Cho hình thoi ABCD có góc B tù. Kẻ BE vuông góc  tại E, BF vuông góc với CD tại F. Gọi M,N lần lượt là giao điểm của BE,BF với AC

Bài 26 trang 99 SBT Toán 8 Tập 1: Cho hình thoi $ABCD$ có góc $B$ tù. Kẻ $BE$ vuông góc $AD$ tại $E$, $BF$ vuông góc với $CD$ tại $F$. Gọi $M,N$ lần lượt là giao điểm của $BE,BF$ với $AC$. Chứng minh tứ giác $BMDN$ là hình thoi.

Trả lời

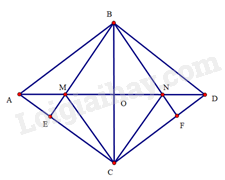
Gọi $O$ là giao điểm của $AC$ và $BD$

Do $ABCD$ là hình thoi nên $AC$ vuông góc với $BD$ tại trung điểm $O$ của $BD$. Suy ra $AC$ là đường trung trực của $BD$. Do đó $BM=DM,BN=DN$.

Do $ABCD$ là hình thoi nên $BA=BC,\widehat{BAE}=\widehat{BCF}$.

Suy ra $\mathrm{\Delta }ABE=\mathrm{\Delta }BCF$ (cạnh huyền – góc nhọn kề)

Do đó $\widehat{ABE}=\widehat{CBF}$. Mà $\widehat{ABD}=\widehat{CBD}$, suy ra $\widehat{MBO}=\widehat{NBO}$.

$\mathrm{\Delta }MBO=\mathrm{\Delta }NBO$ (cạnh góc vuông – góc nhọn). suy ra $BM=BN$

Mà $BM=DM$ và $BN=DN$, suy ra $BM=DM=BN=DN$.

Tứ giác $BMDN$ có $BM=DM=BN=DN$ nên $BMDN$ là hình thoi.

Xem thêm các bài giải SBT Toán 8 Cánh diều hay, chi tiết khác:

Bài 3: Hình thang cân

Bài 4: Hình bình hành

Bài 5: Hình chữ nhật

Bài 6: Hình thoi

Bài 7: Hình vuông

Bài tập cuối chương 5 trang 103