Giải SBT Toán 8 (Cánh diều) Bài 3: Đường trung bình của tam giác

Giải SBT Toán 8 Bài 3: Đường trung bình của tam giác

Giải SBT Toán 8 trang 65

Bài 14 trang 65 SBT Toán 8 Tập 2: Chọn phát biểu đúng trong các phát biểu sau:

a) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng một phần ba cạnh đó.

b) Trong một tam giác chỉ có một đường trung bình.

c) Đường trung bình của tam giác là doạn thẳng nối trung điểm hai cạnh tam giác dó.

d) Đường trung bình của tam giác là đoạn thẳng nối từ một đỉnh đến trung điểm của cạnh đối diện.

Lời giải:

Phát biểu a) là sai do độ dài đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh đó.

Phát biểu b) là sai do trong một tam giác có ba đường trung bình.

Phát biểu c) là đúng.

Phát biểu d) là sai do đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác đó.

Bài 15 trang 65 SBT Toán 8 Tập 2: Hình 21 cho biết cạnh của tam giác đều ABC bằng 6 cm; M, N lần lượt là trung điểm các cạnh AB, AC. Chỉ ra phát biểu sai trong các phát biểu sau:

a) Tam giác AMN là tam giác đều.

b) Hình thang BMNC là hình thang cân.

c) Chu vi tứ giác BMNC bằng hai phần ba chu vi tam giác ABC.

d) Độ dài đường trung bình MN bằng 2 cm.

Lời giải:

• Do M, N lần lượt là trung điểm của AB, AC nên $AM=BM=\frac{1}{2}AB$; $\hspace{0.17em}AN=CN=\frac{1}{2}AC$

Mà AB = AC và $\widehat{BAC}=60°$ (do tam giác ABC đều)

Nên AM = AN và $\widehat{MAN}=60°$

Do đó tam giác AMN là tam giác đều. Do đó phát biểu a) là đúng.

⦁ Xét ∆ABC có M, N lần lượt là trung điểm của AB, AC nên MN là đường trung bình của tam giác nên MN // BC.

Xét tứ giác MNCB có MN // BC nên là hình thang

Lại có $\widehat{B}=\widehat{C}$ (do tam giác ABC đều) nên MNCB là hình thang cân.

Do đó phát biểu b) là đúng.

⦁ Do MN là đường trung bình của tam giác ABC nên $MN=\frac{1}{2}BC=\frac{1}{2}\cdot 6=3$ (cm).

Do đó phát biểu d) là sai.

⦁ Chu vi tam giác ABC là: AB + BC + CA = 6 + 6 + 6 = 18 cm.

Do $AM=BM=\frac{1}{2}AB$; $\hspace{0.17em}AN=CN=\frac{1}{2}AC$ nên BM = NC = 3 cm.

Chu vi tứ giác BMNC là: BM + MN + NC + CB = 3 + 3 + 3 + 6 = 15 (cm).

Vậy tỉ số giữa chu vi tứ giác BMNC và chu vi tam giác ABC là $\frac{15}{18}=\frac{5}{6}.$

Do đó phát biểu c) là sai.

Vậy các phát biểu sai là: c), d).

Bài 16 trang 65 SBT Toán 8 Tập 2: Cho tam giác ABC cân tại A, có M là trung điểm của BC. Kẻ tia Mx song song với AC cắt AB tại E và tia My song song với AB cắt AC tại F. Chứng minh:

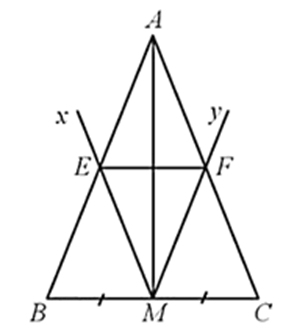
a) EF là đường trung bình của tam giác ABC;

b) AM là đường trung trực của EF.

Lời giải:

a) Xét ∆ABC có M là trung điểm của BC và ME // AC nên E là trung điểm của AB.

Tương tự, do M là trung điểm của BC và MF // AB nên F là trung điểm của AC.

Do đó, EF là đường trung bình của tam giác ABC.

b) Do E, F lần lượt là trung điểm của AB, AC.

Nên ta có $AE=\frac{AB}{2},AF=\frac{AC}{2}$ và AB = AC (do ∆ABC cân tại A) suy ra AE = AF

Do đó A nằm trên đường trung trực của EF (1)

Lại có ME, MF là các đường trung bình của tam giác ABC nên $ME=\frac{AC}{2},MF=\frac{AB}{2}$

Mà AB = AC nên ME = MF

Do đó M nằm trên đường trung trực của EF (2)

Từ (1) và (2) suy ra AM là đường trung trực của EF.

Bài 17 trang 65 SBT Toán 8 Tập 2: Để làm cây thông noel, người ta hàn một khung sắt có dạng hình tam giác cân ABC (AB = AC = 2 m) cùng các thanh sắt nằm ngang GF, HE, ID, BC và sau đó gắn cây thông như Hình 22. Tính số tiền sắt cần sử dụng để làm cây thông noel đó.

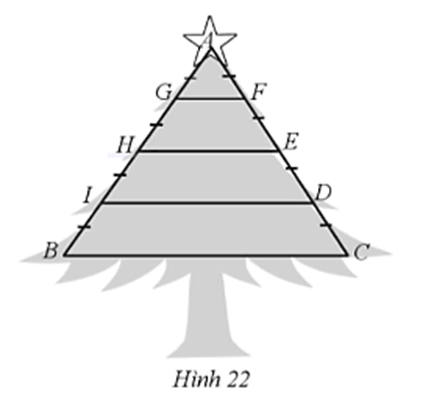
Biết giá một mét sắt là 55 000 đồng và AG = GH = HI = IB, CD = DE = EF = FA, thanh GF dài 0,2 m.

Lời giải:

Do AG = GH nên G là trung điểm của AH.

AF = FE nên F là trung điểm AE.

Xét ∆AHE có G, F lần lượt là trung điểm của AH, AE nên GF là đường trung bình của ∆AHE

Nên HE = 2GF = 2.0,2 = 0,4 (m).

• Do AH = AG + GH, BH = BI + IH, mà AG = GH = BI = IH

Nên AH = BH, hay H là trung điểm của AB.

• Do AE = AF + FE, EC = ED + CD, mà AF = FE = ED = CD

Nên AE = EC, hay E là trung điểm của AC.

Xét ∆ABC có H, E lần lượt là trung điểm của AB, AC nên HE là đường trung bình của ∆ABC, do đó BC = 2HE = 2.0,4 = 0,8 (m).

Ta có AI = 3BI, AB = 4BI nên $\frac{AI}{AB}=\frac{3}{4}$

AD = 3CD, AC = 4CD nên $\frac{AD}{AC}=\frac{3}{4}$

Do đó, $\frac{AI}{AB}=\frac{AD}{AC}=\frac{3}{4}$

Xét ∆ABC có $\frac{AI}{AB}=\frac{AD}{AC}$, theo định lí Thalès đảo ta có ID // BC.

Theo hệ quả của định lí Thalès, ta có $\frac{ID}{BC}=\frac{AI}{AB}=\frac{3}{4}$

Suy ra $ID=\frac{3}{4}BC=\frac{3}{4}\cdot 0,8=0,6$ (m).

Số mét sắt cần sử dụng để làm cây thông noel đó là:

GF + HE + ID + BC + AB + AC = 0,2 + 0,4 + 0,6 + 0,8 + 2 + 2 = 6 (m).

Vậy số tiền cần trả để hoàn thành cây thông noel đó là:

6.55 000 = 330 000 (đồng).

Giải SBT Toán 8 trang 66

Bài 18 trang 66 SBT Toán 8 Tập 2: Cho hình chữ nhật ABCD. Kẻ CH vuông góc với BD (H ∈ BD). Gọi I, K, M lần lượt là trung điềm của BH, CH, AD. Chứng minh:

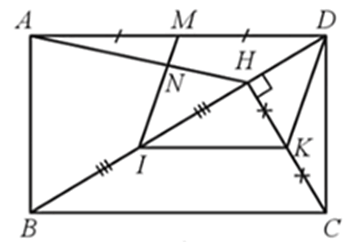
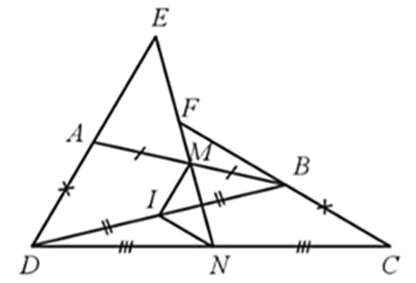
a) Tứ giác IKDM là hình bình hành;

b) Gọi N là giao điểm của IM và AH. Hỏi IN có thể là đường trung bình của tam giác HAB không? Vì sao?

Lời giải:

a) Xét ∆HBC có I, K lần lượt là trung điểm của BH, CH nên IK là đường trung bình của ∆HBC

Suy ra IK // BC và $IK=\frac{BC}{2}.$

Do ABCD là hình chữ nhật nên AD // BC, AD = BC, mà M ∈ AD nên MD // BC

Do đó, IK // MD (1)

Vì $IK=\frac{BC}{2}$ và $MD=\frac{BC}{2}$ (do M là trung điểm của AD, AD = BC) nên IK = MD (2)

Từ (1) và (2) suy ra tứ giác IKDM là hình bình hành.

b) Nếu IN là đường trung bình của tam giác HAB thì IN // AB. Suy ra IM // AB.

Xét ∆ABD có M là trung điểm của AD và IM // AB nên I là trung điểm của BD (3).

Mặt khác, theo giả thiết, I là trung điểm của HB (4).

Từ (3) và (4) suy ra vô lí.

Vậy IN không thể là đường trung bình của tam giác HAB.

Bài 19* trang 66 SBT Toán 8 Tập 2: Cho tứ giác ABCD có AD = BC. Đường thẳng đi qua trung điểm M và N lần lượt của các cạnh AB và CD cắt các đường thẳng AD và BC lần lượt tại E và F. Chứng minh: $\widehat{AEM}=\widehat{MFB}.$

Lời giải:

Lấy I là trung điểm của BD.

Xét ∆ABD có M, I lần lượt là trung điểm của AB, BD nên MI là đường trung bình của ∆ABD

Suy ra MI // AD và $MI=\frac{AD}{2}$ (1)

Xét ∆BDC có N, I lần lượt là trung điểm của CD, BD nên NI là đường trung bình của ∆BDC

Suy ra NI // BC và $NI=\frac{BC}{2}$ (2)

Mà AD = BC (3)

Từ (1), (2), (3) suy ra MI = NI, nên tam giác IMN cân ở I.

Do đó $\widehat{IMN}=\widehat{INM}.$

Lại có $\widehat{IMN}=\widehat{AEM}$ (hai góc đồng vị do IM // AE)

Suy ra $\widehat{INM}=\widehat{AEM}$

Mặt khác $\widehat{INM}=\widehat{MFB}$ (hai góc so le trong do IN // FB).

Suy ra $\widehat{AEM}=\widehat{MFB}.$

Bài 20* trang 66 SBT Toán 8 Tập 2: Cho tứ giác ABCD có M, N lần lượt là trung điểm của AD, BC. Chứng minh: $MN\le \frac{AB+DC}{2}$. Dấu đẳng thức xảy ra khi nào?

Lời giải:

Lấy I là trung điểm của BD.

Xét ∆ABD có M, I lần lượt là trung điểm của AD, BD nên MI là đường trung bình của ∆ABD

Suy ra MI // AB và $MI=\frac{AB}{2}.$

Xét ∆BDC có N, I lần lượt là trung điểm của BC, BD nên NI là đường trung bình của ∆BDC

Suy ra NI // CD và $NI=\frac{CD}{2}.$

Do đó $MI+NI=\frac{AB+CD}{2}$ (1).

• Nếu I không thuộc MN thì MNI là tam giác nên ta có MN < MI + NI (bất đẳng thức tam giác).

• Nếu I thuộc MN ta có MN = MI + NI.

Tức là, ta luôn có MN ≤ MI + NI (2).

Từ (1), (2) suy ra $MN\le \frac{AB+CD}{2}.$

Dấu đẳng thức xảy ra khi I thuộc MN, khi đó AB // MI // CD.

Vậy dấu đẳng thức xảy ra khi AB // CD.

Xem thêm Lời giải bài tập Toán 8 sách Cánh diều hay, chi tiết khác: