Giải SBT Toán 8 (Cánh diều) Bài 1: Định lí Thalès trong tam giác

Giải SBT Toán 8 Bài 1: Định lí Thalès trong tam giác

Giải SBT Toán 8 trang 59

Bài 1 trang 59 SBT Toán 8 Tập 2: Cho các đoạn thẳng AB = 6 cm, CD = 4 cm, PQ = 8 cm, EF = 10 cm, MN = 25 cm, RS = 15 cm. Tìm phát biểu đúng trong các phát biểu sau:

a) Hai đoạn thẳng AB và PQ tỉ lệ với hai đoạn thẳng EF và RS.

b) Hai đoạn thẳng AB và RS tỉ lệ với hai đoạn thẳng EF và MN.

c) Hai đoạn thẳng AB và CD tỉ lệ với hai đoạn thẳng PQ và EF.

Lời giải:

⦁ Ta có $\frac{AB}{PQ}=\frac{6}{8}=\frac{3}{4}; \frac{EF}{RS}=\frac{10}{15}=\frac{2}{3}.$

Do đó hai đoạn thẳng AB và PQ không tỉ lệ với hai đoạn thẳng EF và RS.

⦁ Ta có $\frac{AB}{RS}=\frac{6}{15}=\frac{2}{5}; \frac{EF}{MN}=\frac{10}{25}=\frac{2}{5}.$

Do đó hai đoạn thẳng AB và RS tỉ lệ với hai đoạn thẳng EF và MN.

⦁ Ta có $\frac{AB}{CD}=\frac{6}{4}=\frac{3}{2}; \frac{PQ}{EF}=\frac{8}{10}=\frac{4}{5}.$

Do đó, hai đoạn thẳng AB và CD không tỉ lệ với hai đoạn thẳng PQ và EF.

Vậy phát biểu b là đúng.

Bài 2 trang 59 SBT Toán 8 Tập 2: Cho các đoạn thẳng EF = 6 cm, GH = 3 cm, IK = 5 cm, MN = x cm. Tìm x để hai đoạn thẳng EF và GH tỉ lệ với hai đoạn thẳng IK và MN.

Lời giải:

Để hai đoạn thẳng EF và GH tỉ lệ với hai đoạn thẳng IK và MN thì $\frac{EF}{GH}=\frac{IK}{MN}$

Thay EF = 6 cm, GH = 3 cm, IK = 5 cm, MN = x cm, ta có $\frac{6}{3}=\frac{5}{x}$

Suy ra $x=\frac{3\cdot 5}{6}=2,5$ (cm)

Vậy x = 2,5 cm.

Bài 3 trang 59 SBT Toán 8 Tập 2: Cho tam giác ABC. Một đường thẳng d song song với BC và cắt các cạnh AB, AC của tam giác đó lần lượt tại M, N với $\frac{AM}{AB}=\frac{1}{3}$ và AN + AC = 16 cm. Tính AN.

Lời giải:

Xét ∆ABC với MN // BC, ta có: $\frac{AM}{AB}=\frac{AN}{AC}=\frac{1}{3}$ (định lí Thalès)

Do đó $\frac{AN}{1}=\frac{AC}{3}=\frac{AN+AC}{1+3}=\frac{16}{4}=4$

Suy ra AN = 4 cm.

Giải SBT Toán 8 trang 60

Bài 4 trang 60 SBT Toán 8 Tập 2: Toà nhà Bitexco Financial (hay tháp tài chinh Bitexco) được xây dụng tại trung tâm Quận 1, Thành phố Hồ Chí Minh. Toà nhà có 68 tầng (không kể các tầng hầm). Biết rằng khi toà nhà có bóng MP in trên mặt đất dài 47,5 m, thì cùng thời điểm đó một cột cờ AB cao 12 m có bóng AP in trên mặt đất dài 2,12 m (Hình 8). Tính chiều cao MN của toà nhà theo đon vị mét (làm tròn kết quả đến hàng đơn vị).

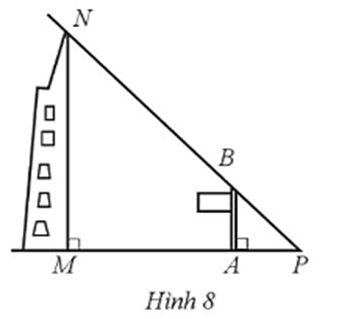
Lời giải:

Tòa nhà MN và cột cờ AB cùng vuông góc với mặt đất nên MN // AB.

Xét ∆MNP với MN // AB, ta có: $\frac{AB}{MN}=\frac{AP}{MP}$ (hệ quả của định lí Thalès)

Hay $\frac{12}{MN}=\frac{2,12}{47,5}$.

Suy ra $MN=\frac{12\cdot 47,5}{2,12}\approx 269$.

Vậy chiều cao MN của toà nhà là 269 m.

Bài 5 trang 60 SBT Toán 8 Tập 2: Cho tam giác ABC vuông ở A. Vẽ ra phía ngoài tam giác đó các tam giác BAD vuông cân ở B, ACF vuông cân ở C. Gọi H là giao điểm của AB và DC, K là giao điểm của AC và BF (Hình 9). Chứng minh:

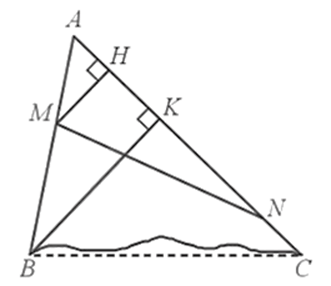
a) AH = AK;

b) AH² = AK² = HB.KC.

Lời giải:

a) Đặt AB = c, AC = b.

Xét ∆BDH với BD // AC (cùng vuông góc với AB), ta có:

$\frac{AH}{HB}=\frac{AC}{BD}$ (hệ quả của định lí Thalès)

Mà BD = AB (do ∆ABD vuông cân tại B) nên $\frac{AH}{HB}=\frac{AC}{BD}=\frac{AC}{AB}=\frac{b}{c}$

Suy ra $\frac{AH}{AH+HB}=\frac{b}{b+c}$ hay $\frac{AH}{AB}=\frac{b}{b+c}$.

Do đó $AH=\frac{bc}{b+c}$ (1)

Tương tự, ∆ABK với AB // CF (cùng vuông góc với AC) và CF = AC (do ∆ACF vuông cân tại C), theo hệ quả của định lí Thalès ta có: $\frac{AK}{KC}=\frac{AB}{CF}=\frac{AB}{AC}=\frac{c}{b}.$

Suy ra $\frac{AK}{KC+AK}=\frac{c}{b+c}$

Hay $\frac{AK}{AC}=\frac{c}{b+c}.$

Do đó $AK=\frac{bc}{b+c}$ (2).

Từ (1) và (2) suy ra: AH = AK.

b) Từ $\frac{AH}{HB}=\frac{AC}{BD}=\frac{b}{c}$ và $\frac{AK}{KC}=\frac{AB}{CF}=\frac{c}{b}$ (câu a), ta có $\frac{AH}{HB}=\frac{KC}{AK}$

Mà AK = AH nên $\frac{AH}{HB}=\frac{KC}{AH}$

Do đó, AH² = AK² = HB.KC.

Bài 6 trang 60 SBT Toán 8 Tập 2: Trong Hình 10, cho biết ABCD là hình thang, AB // CD (AB < CD); M là trung điểm của DC; AM cắt BD ở I; BM cắt AC ở K; IK cắt AD, BC lần lượt ở E, F. Chứng minh:

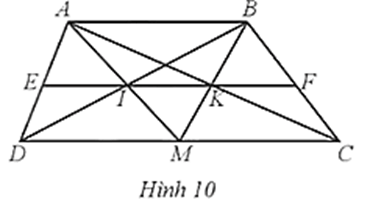
a) IK // AB;

b) EI = IK = KF.

Lời giải:

a) Vì M là trung điểm của CD nên DM = MC.

Do AB // CD, M ∈ CD nên AB // DM, AB // CM.

Xét ∆IDM với AB // DM, ta có: $\frac{IA}{IM}=\frac{AB}{DM}=\frac{AB}{MC}$ (do DM = MC) (1)

Xét ∆MKC với AB // CM, ta có: $\frac{KB}{KM}=\frac{AB}{MC}$ (2).

Từ (1) và (2) suy ra $\frac{IA}{IM}=\frac{KB}{KM}$

Xét ∆ABM có $\frac{IA}{IM}=\frac{KB}{KM}$ nên IB // AB (định lí Thalès đảo).

b) Áp dụng định lí Thalès cho ∆ADM với EI // DM, ta có $\frac{EI}{DM}=\frac{AI}{AM}$ (3)

Áp dụng định lí Thales cho ∆AMB với IK // AB, ta có $\frac{AI}{AM}=\frac{BK}{BM}$

Áp dụng định lí Thales cho ∆BMC với KF // MC, ta có $\frac{BK}{BM}=\frac{KF}{MC}$

Do đó, ta có: $\frac{EI}{DM}=\frac{AI}{AM}=\frac{BK}{BM}=\frac{KF}{MC}$.

Suy ra EI = KF (do DM = MC). (*)

Mặt khác, áp dụng định lí Thalès cho ∆AMC với IK // MC, ta có: $\frac{IK}{MC}=\frac{AI}{AM}$ (4)

Từ (3) và (4) suy ra $\frac{IK}{MC}=\frac{EI}{DM}$ hay IK = EI (do MC = DM). (**)

Từ (*) và (**) suy ra EI = IK = KF

Bài 7 trang 60 SBT Toán 8 Tập 2: Cho ABCD là hình bình hành. Một đường thẳng d đi qua A cắt BD, BC, DC lần lượt tại E, K, G (Hình 11). Chứng minh:

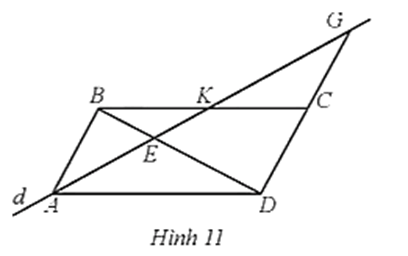
a) AE² = EK.EG;

b) $\frac{1}{AE}=\frac{1}{AK}+\frac{1}{AG}.$

Lời giải:

a) Do ABCD là hình bình hành nên AB // CD, AD // BC.

Mà K ∈ BC, G ∈ CD nên AD // BK, AB // DG.

Xét ∆AED với BK // AD, ta có $\frac{EK}{EA}=\frac{EB}{ED}$ (hệ quả của định lí Thalès)

Xét ∆EDG với AB // DG, ta có $\frac{EB}{ED}=\frac{EA}{EG}$ (hệ quả của định lí Thalès)

Suy ra $\frac{EK}{EA}=\frac{EA}{EG}$ nên AE² = EK.EG.

b) Xét ∆ADE với BK // AD, ta có $\frac{AE}{AK}=\frac{DE}{DB}$ (hệ quả của định lí Thalès)

Xét ∆EDG với AB // DG, ta có $\frac{AE}{AG}=\frac{BE}{BD}$ (hệ quả của định lí Thalès)

Suy ra $\frac{AE}{AK}+\frac{AE}{AG}=\frac{DE}{DB}+\frac{BE}{BD}=\frac{BD}{BD}=1$

Do đó $AE\cdot \left(\frac{1}{AK}+\frac{1}{AG}\right)=1$

Vậy $\frac{1}{AE}=\frac{1}{AK}+\frac{1}{AG}.$

Bài 8 trang 60 SBT Toán 8 Tập 2: An có một mảnh bìa có dạng hình tam giác ABC nhưng bị rách. An muốn cắt bỏ phần bị rách với vết cắt là đoạn thẳng MN. Tính diện tích tứ giác MNCB theo diện tích tam giác ABC, biết $\frac{AM}{MB}=\frac{2}{3}$ và $\frac{NC}{NA}=\frac{1}{5}$ (Hình 12).

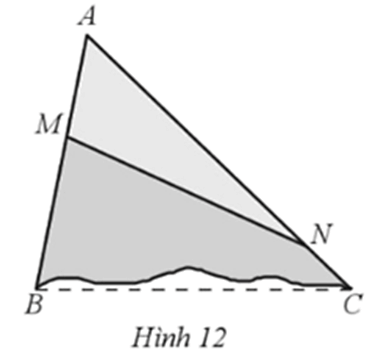
Lời giải:

Kẻ đường cao MH của tam giác AMN và đường cao BK của tam giác ABC.

Do đó MH // BK (cùng vuông góc với AC).

Xét ∆ABK với MH // BK, ta có $\frac{MH}{BK}=\frac{AM}{AB}$ (hệ quả của định lí Thalès)

Bài 9* trang 60 SBT Toán 8 Tập 2: Cho tam giác ABC có ba góc nhọn, đường cao AH. Trên AH, AB, AC lần lượt lấy các điểm D, E, F sao cho $\widehat{EDC}=\widehat{FDB}=90°$. Chứng minh: EF // BC.

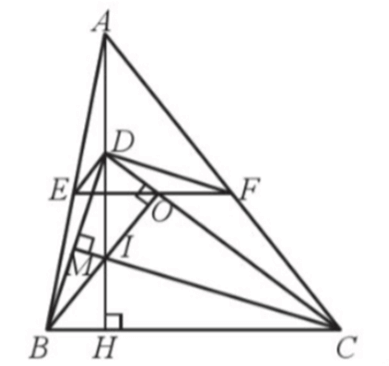
Lời giải:

Kẻ BO ⊥ CD, CM ⊥ BD, BO cắt CM tại I , suy ra D là trực tâm của ∆BIC hay DI ⊥ BC.

Mặt khác, AH ⊥ BC suy ra I, D, A thẳng hàng.

Do $\widehat{EDC}=\widehat{FDB}=90°$ nên ED ⊥ DC, DF ⊥ DB

Ta có: ED ⊥ DC, BO ⊥ CD, I ∈ BO nên ED // BI;

DF ⊥ DB, CM ⊥ BD, I ∈ CM nên DF // CI.

Xét ∆ABI với DE // BI, ta có: $\frac{AD}{AI}=\frac{AE}{AB}$ (hệ quả của định lí Thalès)

Xét ∆ACI với DF // IC, ta có: $\frac{AD}{AI}=\frac{AF}{AC}$ (hệ quả của định lí Thalès)

Suy ra $\frac{AE}{AB}=\frac{AF}{AC}.$

Xét ∆ABC có $\frac{AE}{AB}=\frac{AF}{AC}$ nên EF// BC (định lí Thalès đảo).

Xem thêm Lời giải bài tập Toán 8 sách Cánh diều hay, chi tiết khác: