Bài 18 trang 66 SBT Toán 8 Tập 2: Cho hình chữ nhật ABCD. Kẻ CH vuông góc với BD (H ∈ BD). Gọi I, K, M lần lượt là trung điềm của BH, CH, AD. Chứng minh:
a) Tứ giác IKDM là hình bình hành;
b) Gọi N là giao điểm của IM và AH. Hỏi IN có thể là đường trung bình của tam giác HAB không? Vì sao?
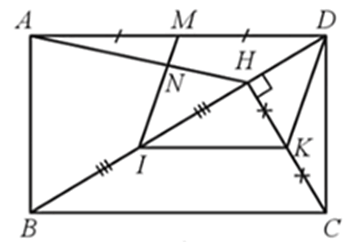
a) Xét ∆HBC có I, K lần lượt là trung điểm của BH, CH nên IK là đường trung bình của ∆HBC
Suy ra IK // BC và
Do ABCD là hình chữ nhật nên AD // BC, AD = BC, mà M ∈ AD nên MD // BC
Do đó, IK // MD (1)
Vì và (do M là trung điểm của AD, AD = BC) nên IK = MD (2)
Từ (1) và (2) suy ra tứ giác IKDM là hình bình hành.
b) Nếu IN là đường trung bình của tam giác HAB thì IN // AB. Suy ra IM // AB.
Xét ∆ABD có M là trung điểm của AD và IM // AB nên I là trung điểm của BD (3).
Mặt khác, theo giả thiết, I là trung điểm của HB (4).
Từ (3) và (4) suy ra vô lí.
Vậy IN không thể là đường trung bình của tam giác HAB.
Xem thêm các bài giải SBT Toán 8 Cánh diều hay, chi tiết khác:
Bài 1: Định lí Thalès trong tam giác
Bài 2: Ứng dụng của định lí Thalès trong tam giác
Bài 3: Đường trung bình của tam giác