Giải SBT Toán 8 Bài 2: Ứng dụng của định lí Thalès trong tam giác
Giải SBT Toán 8 trang 62
Lời giải:
Đổi 2 phút 42 giây = 2710 phút.
Khi đó độ dài CD là CD=100⋅2710=270 (m).
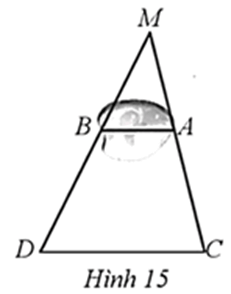
Do MB=45BD nên MBBD=45, do đó MBBD+MB=45+4 hay MBMD=49
Xét ∆MCD với AB // CD, ta có: ABCD=MBMD=49 (hệ quả của định lí Thalès)
Hay AB=49CD.
Vậy độ dài AB là: AB=49⋅270=120 (m).
Lời giải:
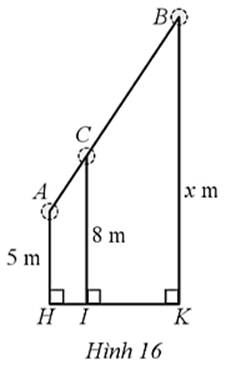
Do AC=25CB nên ACCB=25, do đó ACCB+AC=25+2 hay ACAB=27
Suy ra 1−ACAB=1−27 hay AB−ACAB=57 nên CBAB=57.
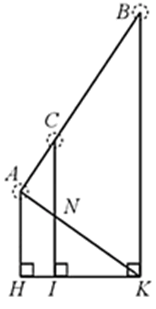
Gọi N là giao điểm của AK và CI.
Xét ∆AKB với CN // BK, ta có: ACAB=CNBK (hệ quả của định lí Thalès)
Hay CNx=27
Suy ra CN=27x (1)
Xét ∆AHK với IN // AH, ta có: NIAH=KIKH=KNKA (hệ quả của định lí Thalès)
Xét ∆AKB với CN // BK, ta có: KNKA=BCBA (hệ quả của định lí Thalès)
Do đó NIAH=KIKH=KNKA=BCBA=57 hay NI5=57
Suy ra NI=5⋅57=257 (m) (2)
Từ (1) và (2) ta có: CI=CN+NI=27x+257
Lại có CI = 8 m nên 27x+257=8
Do đó 27x=8−257
27x=317
x=317:27
x=312
x = 15,5.
Vậy x = 15,5.
Giải SBT Toán 8 trang 63
Lời giải:
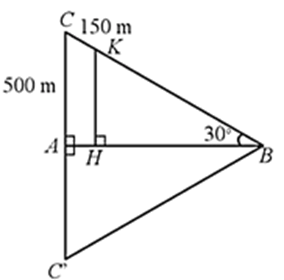
Trên tia đối của tia AC lấy C’ sao cho AC’ = AC.
Xét ∆ACB (vuông tại A) và ∆AC’B (vuông tại A) có:
^CAB=C'
AB là cạnh chung;
AC = AC’ (theo cách vẽ)
Khi đó ∆ACB = ∆AC’B (hai cạnh góc vuông)
Suy ra BC = BC’ (hai cạnh tương ứng) và (hai góc tương ứng)
Tam giác BCC’ có BC = BC’ và = 30° + 30° = 60° nên BCC’ là tam giác đều.
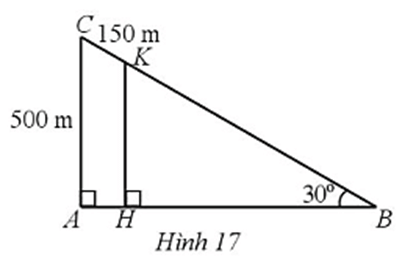
Suy ra CB = CC’ = 2.CA = 5.500 = 1 000 (m).
Do đó KB = CB ‒ CK = 1 000 ‒ 150 = 850 (m).
Xét ∆ABC với KH // CA, ta có: (hệ quả của định lí Thalès)
Hay
Suy ra (m).
Vậy độ cao KH bằng 425 m.
Lời giải:
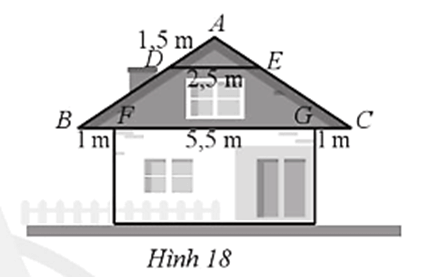
Ta có BC = BF + FG + GC = 1 + 5,5 + 1 = 7,5 (m).
BC với DE // BC, ta có: (hệ quả của định lí Thalès)
Hay .
Suy ra m.
Vậy chiều dài AB của mái nhà là 4,5 m.
Xem thêm Lời giải bài tập Toán 8 sách Cánh diều hay, chi tiết khác: