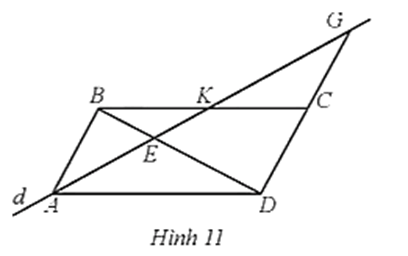
Cho ABCD là hình bình hành. Một đường thẳng d đi qua A cắt BD, BC, DC lần lượt tại E, K, G (Hình 11)

Bài 7 trang 60 SBT Toán 8 Tập 2: Cho ABCD là hình bình hành. Một đường thẳng d đi qua A cắt BD, BC, DC lần lượt tại E, K, G (Hình 11). Chứng minh:

a) AE² = EK.EG;

b) $\frac{1}{AE}=\frac{1}{AK}+\frac{1}{AG}.$

Trả lời

a) Do ABCD là hình bình hành nên AB // CD, AD // BC.

Mà K ∈ BC, G ∈ CD nên AD // BK, AB // DG.

Xét ∆AED với BK // AD, ta có $\frac{EK}{EA}=\frac{EB}{ED}$ (hệ quả của định lí Thalès)

Xét ∆EDG với AB // DG, ta có $\frac{EB}{ED}=\frac{EA}{EG}$ (hệ quả của định lí Thalès)

Suy ra $\frac{EK}{EA}=\frac{EA}{EG}$ nên AE² = EK.EG.

b) Xét ∆ADE với BK // AD, ta có $\frac{AE}{AK}=\frac{DE}{DB}$ (hệ quả của định lí Thalès)

Xét ∆EDG với AB // DG, ta có $\frac{AE}{AG}=\frac{BE}{BD}$ (hệ quả của định lí Thalès)

Suy ra $\frac{AE}{AK}+\frac{AE}{AG}=\frac{DE}{DB}+\frac{BE}{BD}=\frac{BD}{BD}=1$

Do đó $AE\cdot \left(\frac{1}{AK}+\frac{1}{AG}\right)=1$

Vậy $\frac{1}{AE}=\frac{1}{AK}+\frac{1}{AG}.$

Xem thêm các bài giải SBT Toán 8 Cánh diều hay, chi tiết khác:

Bài 2: Ứng dụng của phương trình bậc nhất một ẩn

Bài tập cuối chương 7

Bài 1: Định lí Thalès trong tam giác

Bài 2: Ứng dụng của định lí Thalès trong tam giác

Bài 3: Đường trung bình của tam giác

Bài 4: Tính chất đường phân giác của tam giác