Cho tam giác ABC có ba góc nhọn, đường cao AH. Trên AH, AB, AC lần lượt lấy các điểm D, E, F sao cho góc EDC = góc FDB = 90 độ 

Bài 9* trang 60 SBT Toán 8 Tập 2: Cho tam giác ABC có ba góc nhọn, đường cao AH. Trên AH, AB, AC lần lượt lấy các điểm D, E, F sao cho $\widehat{EDC}=\widehat{FDB}=90°$. Chứng minh: EF // BC.

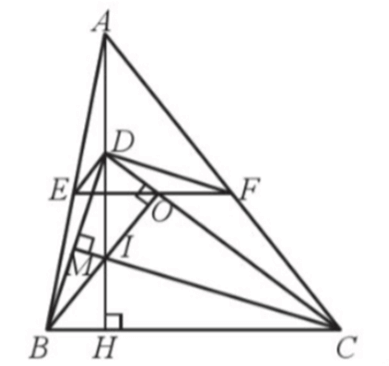
Trả lời

Kẻ BO ⊥ CD, CM ⊥ BD, BO cắt CM tại I , suy ra D là trực tâm của ∆BIC hay DI ⊥ BC.

Mặt khác, AH ⊥ BC suy ra I, D, A thẳng hàng.

Do $\widehat{EDC}=\widehat{FDB}=90°$ nên ED ⊥ DC, DF ⊥ DB

Ta có: ED ⊥ DC, BO ⊥ CD, I ∈ BO nên ED // BI;

DF ⊥ DB, CM ⊥ BD, I ∈ CM nên DF // CI.

Xét ∆ABI với DE // BI, ta có: $\frac{AD}{AI}=\frac{AE}{AB}$ (hệ quả của định lí Thalès)

Xét ∆ACI với DF // IC, ta có: $\frac{AD}{AI}=\frac{AF}{AC}$ (hệ quả của định lí Thalès)

Suy ra $\frac{AE}{AB}=\frac{AF}{AC}.$

Xét ∆ABC có $\frac{AE}{AB}=\frac{AF}{AC}$ nên EF// BC (định lí Thalès đảo).