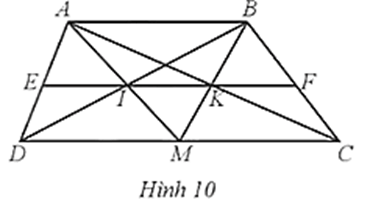
Trong Hình 10, cho biết ABCD là hình thang, AB // CD (AB < CD); M là trung điểm của DC; AM cắt BD ở I; BM cắt AC ở K; IK cắt AD, BC lần lượt ở E, F

Bài 6 trang 60 SBT Toán 8 Tập 2: Trong Hình 10, cho biết ABCD là hình thang, AB // CD (AB < CD); M là trung điểm của DC; AM cắt BD ở I; BM cắt AC ở K; IK cắt AD, BC lần lượt ở E, F. Chứng minh:

a) IK // AB;

b) EI = IK = KF.

Trả lời

a) Vì M là trung điểm của CD nên DM = MC.

Do AB // CD, M ∈ CD nên AB // DM, AB // CM.

Xét ∆IDM với AB // DM, ta có: $\frac{IA}{IM}=\frac{AB}{DM}=\frac{AB}{MC}$ (do DM = MC) (1)

Xét ∆MKC với AB // CM, ta có: $\frac{KB}{KM}=\frac{AB}{MC}$ (2).

Từ (1) và (2) suy ra $\frac{IA}{IM}=\frac{KB}{KM}$

Xét ∆ABM có $\frac{IA}{IM}=\frac{KB}{KM}$ nên IB // AB (định lí Thalès đảo).

b) Áp dụng định lí Thalès cho ∆ADM với EI // DM, ta có $\frac{EI}{DM}=\frac{AI}{AM}$ (3)

Áp dụng định lí Thales cho ∆AMB với IK // AB, ta có $\frac{AI}{AM}=\frac{BK}{BM}$

Áp dụng định lí Thales cho ∆BMC với KF // MC, ta có $\frac{BK}{BM}=\frac{KF}{MC}$

Do đó, ta có: $\frac{EI}{DM}=\frac{AI}{AM}=\frac{BK}{BM}=\frac{KF}{MC}$.

Suy ra EI = KF (do DM = MC). (*)

Mặt khác, áp dụng định lí Thalès cho ∆AMC với IK // MC, ta có: $\frac{IK}{MC}=\frac{AI}{AM}$ (4)

Từ (3) và (4) suy ra $\frac{IK}{MC}=\frac{EI}{DM}$ hay IK = EI (do MC = DM). (**)

Từ (*) và (**) suy ra EI = IK = KF

Xem thêm các bài giải SBT Toán 8 Cánh diều hay, chi tiết khác:

Bài 2: Ứng dụng của phương trình bậc nhất một ẩn

Bài tập cuối chương 7

Bài 1: Định lí Thalès trong tam giác

Bài 2: Ứng dụng của định lí Thalès trong tam giác

Bài 3: Đường trung bình của tam giác

Bài 4: Tính chất đường phân giác của tam giác