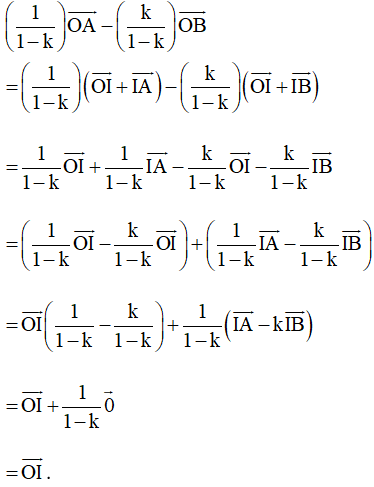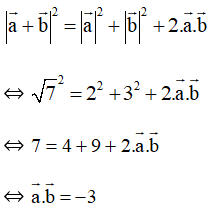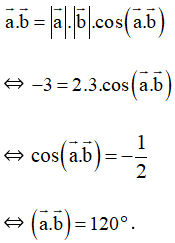Giải Sách bài tập Toán 10 Bài ôn tập chương 4
Giải SBT Toán 10 trang 106 Tập 1
Bài 67 trang 106 SBT Toán 10 Tập 1: Cho góc nhọn α. Biểu thức (sinα . cotα)2 + (cosα . tanα)2 bằng:
A. 2.
B. tan2α + cot2α.
C. 1.
D. sinα + cosα.
Lời giải:
Đáp án đúng là C
Ta có: (sinα . cotα)2 + (cosα . tanα)2
= (sinα.)2 + (cosα.)2
= cos2α + sin2α
= 1.
Bài 68 trang 106 SBT Toán 10 Tập 1: Cho các vectơ . Phát biểu nào sau đây là đúng?
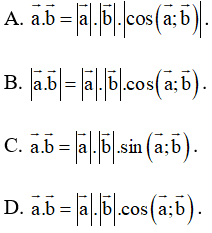
Lời giải:
Đáp án đúng là D
Với ta có: .
Bài 69 trang 106 SBT Toán 10 Tập 1: Cho tứ giác ABCD. Biểu thức bằng:
A. CD2.
B. 0.
C.  .
.
D. 1.
Lời giải:
Đáp án đúng là B
Ta có:
Bài 70 trang 106 SBT Toán 10 Tập 1: Cho góc nhọn α. Biểu thức tanα . tan(90°– α) bằng:
A. tanα + cotα.
B. tan2α
C. 1.
D. tan2α + cot2α.
Lời giải:
Đáp án đúng là C
tanα . tan(90°– α)
= tanα . cotα
= 1.
Bài 71 trang 106 SBT Toán 10 Tập 1: Cho α thỏa mãn . Tính cosα, tanα, cotα, sin(90° – α), cos(90° – α), sin(180° – α), cos(180° – α) trong các trường hợp sau:
a) 0° < α < 90°;
b) 90° < α < 180°;
Lời giải:
Ta có:

a) Vì 0° < α < 90° nên
⇒
⇒
Áp dụng công thức lượng giác của hai góc bù nhau, ta được:
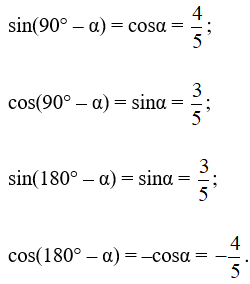
b) Vì 90° < α < 180° nên
⇒
⇒
Áp dụng công thức lượng giác của hai góc bù nhau, ta được:
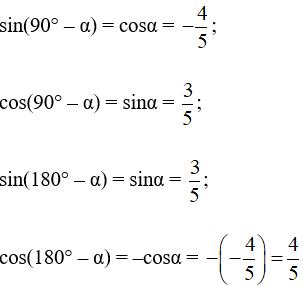
Giải SBT Toán 10 trang 107 Tập 1
Bài 72 trang 107 SBT Toán 10 Tập 1: Cho tam giác ABC có AB = 4, AC = 6, . Tính (làm tròn kết quả đến hàng đơn vị):
a) Độ dài cạnh BC và độ lớn góc B;
b) Bán kính đường tròn ngoại tiếp R;
c) Diện tích của tam giác ABC;
d) Độ dài đường cao xuất phát từ A;
e) với M là trung điểm của BC.
Lời giải:
a) Độ dài cạnh BC và độ lớn góc B;
Xét tam giác ABC, có:
BC2 = AB2 + AC2 – 2AB.AC.cos
= 42 + 62 – 2.4.6.cos60°
= 42 + 62 – 24
= 28
⇔ BC = .
Áp dụng định lí sin trong tam giác ABC ta được:
⇔
⇔ .
Vậy BC = và .
b) Áp dụng định lí sin trong tam giác, ta có:
⇔ .
Vậy bán kính đường tròn ngoại tiếp tam giác ABC là 3.
c) Áp dụng công thức tính diện tích tam giác, ta được:
Vậy diện tích của tam giác ABC là (đvdt).
d) Gọi AH là đường cao của tam giác kẻ từ đỉnh A
Ngoài ra diện tích tam giác ABC là:
Theo ý c) ta tính được diện tích tam giác là
Do đó ta có:
⇔
Vậy độ dài đường cao xuất phát từ A là 4.
e) Ta có:
Vì M là trung điểm của BC nên
Khi đó:
Vậy và .
Bài 73 trang 107 SBT Toán 10 Tập 1: Cho tam giác ABC. Chứng minh rằng .
Lời giải:
Ta có:
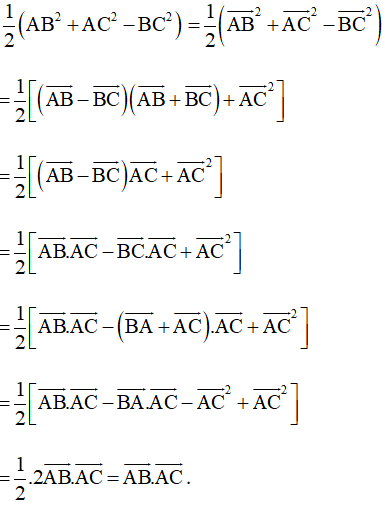
Bài 74 trang 107 SBT Toán 10 Tập 1: Cho tam giác ABC có AB = 5, BC = 6, CA = 7. Tính:
a) ;
b) Diện tích tam giác ABC;
c) Độ dài đường trung tuyến AM.
Lời giải:
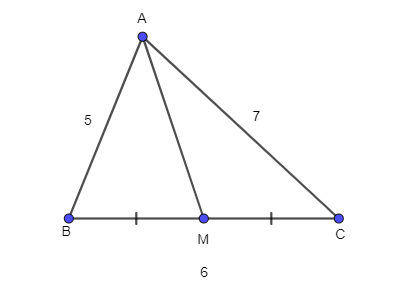
a) Xét tam giác ABC, có:
Áp dụng hệ quả của định lí cosin, ta được:
Ta có:
⇔
Vì là góc trong tam giác nên
⇒ .
Vậy .
b) Diện tích tam giác ABC là:
Vậy diện tích tam giác ABC là
c) Vì M là trung điểm của BC nên BM = MC = BC = .6 = 3.
Xét tam giác ABM:
Áp dụng định lí cos, ta có:
AM2 = AB2 + BM2 – 2.AM.BM.cosB
⇔ AM2 = 52 + 32 – 2.5.3.
⇔ AM2 = 28
⇔ AM =
Vậy độ dài đường trung tuyến AM là .
Bài 75 trang 107 SBT Toán 10 Tập 1: Cho ba điểm I, A, B và số thực k ≠ 1 thỏa mãn . Chứng minh với O là điểm bất kì ta có: .
Lời giải:
Ta có:
Xét vế phải của đẳng thức ta có:
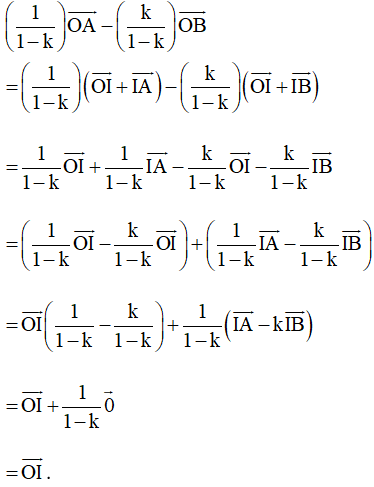
Bài 76 trang 107 SBT Toán 10 Tập 1: Cho tam giác ABC có AB = 4, AC = 5, . Điểm M là trung điểm của đoạn thẳng BC, điểm D thỏa mãn . Tính tích vô hướng và chứng minh AM ⊥ BD.
Lời giải:
Ta có:
Ta lại có:
Và
⇒
⇔
⇔
Suy ra AM vuông góc BD.
Vậy và AM vuông góc BD.
Bài 77 trang 107 SBT Toán 10 Tập 1: Một người quan sát đứng ở bờ sông muốn đo độ rộng của khúc sông chỗ chảy qua vị trí đứng (khúc sông tương đối thẳng, có thể xem hai bờ sông song song).
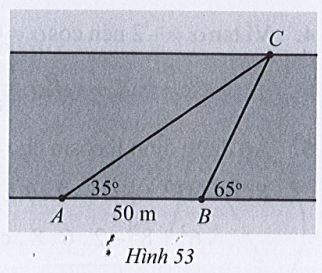
Từ vị trí đang đứng A, người đó đo được góc nghiêng α = 35° so với bờ sông tới một vị trí C quan sát được ở phía bờ bên kia. Sau đi dọc bờ sông đến vị trí B cách A một khoảng d = 50m và tiếp tục đo được góc nghiêng β = 65° so với bờ sông tới vị trí C đã chọn (Hình 53). Hỏi độ rộng của con sông chỗ chảy qua vị trí người quan sát đang đứng là bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?
Lời giải:
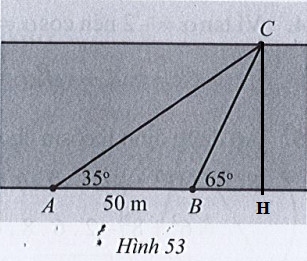
Kẻ CH vuông góc với bờ AB.
Xét tam giác ABC, có:
⇒
Áp dụng định lí sin trong tam giác, ta được:
⇔
⇔
Xét tam giác CHB vuông tại B, có:
.
Vậy độ rộng của con sông chỗ chảy qua vị trí người quan sát khoảng 51,98 mét.
Bài 78 trang 107 SBT Toán 10 Tập 1: Cho hai vectơ và . Tính .
Lời giải:
Giải SBT Toán 10 trang 108 Tập 1
Bài 79 trang 108 SBT Toán 10 Tập 1: a) Chứng minh đẳng thức với và là hai vectơ bất kì.
b) Cho . Tính và .
Lời giải:
a)
b) Áp dụng công thức trên ta được:
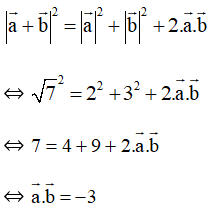
Mặt khác ta lại có:
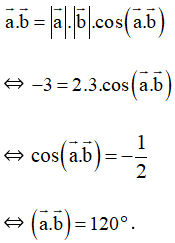
Vậy và .
Bài 80 trang 108 SBT Toán 10 Tập 1: Cho tam giác ABC, có ba trung tuyến AD, BE, CF. Chứng minh rằng: .
Lời giải:
Ta có:
=
=
=
= 0
Bài 81 trang 108 SBT Toán 10 Tập 1: Cho tứ giác ABCD, M là điểm thay đổi trong mặt phẳng thỏa mãn . Chứng minh M luôn nằm trên đường tròn cố định.
Lời giải:
Gọi I và J lần lượt là trung điểm của AB và CD.
Khi đó ta có: và
⇒
⇔
⇔
⇔
⇔
Vậy M là điểm thuộc đường tròn đường kính IJ.
Bài 82 trang 108 SBT Toán 10 Tập 1: Cho tam giác ABC và đường thẳng d không có điểm chung với bất kì cạnh nào của tam giác. M là điểm thay đổi trên đường thẳng d. Xác định vị trí của M sao cho biểu thức đạt giá trị nhỏ nhất.
Lời giải:
Xét biểu thức
⇒
Do đó để biểu thức đạt giá trị nhỏ nhất thì đạt giá trị nhỏ nhất khi MG nhỏ nhất và MG nhỏ nhất khi M là hình chiếu vuông góc của G lên đường thẳng d.
Vậy để đạt giá trị nhỏ nhất thì điểm M là hình chiếu vuông góc của G trên đường thẳng d.
Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:
Bài 5: Tích của một số với một vectơ
Bài 6: Tích vô hướng của hai vectơ
Bài 1: Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây
Bài 2: Hoán vị. Chỉnh hợp
Bài 3: Tổ hợp
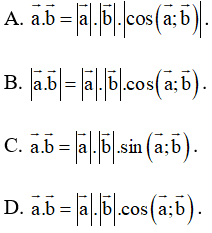
![]() .
.
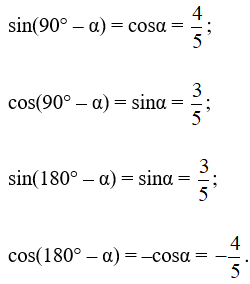
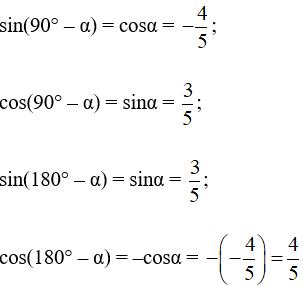
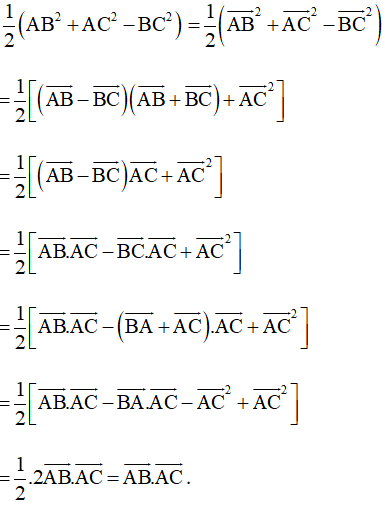

![]()