a) Chứng minh đẳng thức |a + b|^2 = |a|^2 + |b|^2 + 2.a.b với a và b là hai vectơ bất kì

Bài 79 trang 108 SBT Toán 10 Tập 1: a) Chứng minh đẳng thức ${\left|\overrightarrow{a}+\overrightarrow{b}\right|}^2={\left|\overrightarrow{a}\right|}^2+{\left|\overrightarrow{b}\right|}^2+2.\overrightarrow{a}.\overrightarrow{b}$ với $\overrightarrow{a}$ và $\overrightarrow{b}$ là hai vectơ bất kì.

b) Cho $\left|\overrightarrow{a}\right|=2,\left|\overrightarrow{b}\right|=3,\left|\overrightarrow{a}+\overrightarrow{b}\right|=\sqrt{7}$. Tính $\overrightarrow{a}.\overrightarrow{b}$ và $\left(\overrightarrow{a},\overrightarrow{b}\right)$.

Trả lời

a) 

$$\begin{gathered} {\left|\overrightarrow{a}+\overrightarrow{b}\right|}^2={\left(\overrightarrow{a}+\overrightarrow{b}\right)}^2 \\ ={\overrightarrow{a}}^2+{\overrightarrow{b}}^2+2.\overrightarrow{a}.\overrightarrow{b} \\ ={\left|\overrightarrow{a}\right|}^2+{\left|\overrightarrow{b}\right|}^2+2.\overrightarrow{a}.\overrightarrow{b} \end{gathered}$$

b) Áp dụng công thức trên ta được:

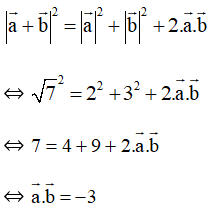
Mặt khác ta lại có: 

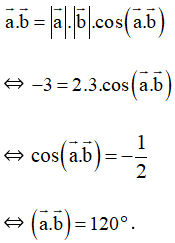
Vậy $\overrightarrow{a}.\overrightarrow{b}=-3$ và $\left(\overrightarrow{a}.\overrightarrow{b}\right)=120°$.

Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài 5: Tích của một số với một vectơ

Bài 6: Tích vô hướng của hai vectơ

Bài ôn tập chương 4

Bài 1: Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây

Bài 2: Hoán vị. Chỉnh hợp

Bài 3: Tổ hợp