Giải Sách bài tập Toán 10 Bài ôn tập chương 1 trang 16
Giải SBT Toán 10 trang 16 Tập 1
Bài 41 trang 16 SBT Toán 10 Tập 1: Phát biểu nào sau đây không là mệnh đề toán học?
A. Số 2 025 chia hết cho 5.
B. Nếu hình thang ABCD nội tiếp đường tròn thì hình thang đó cân.
C. Nếu bạn Minh chăm chỉ thì bạn Minh sẽ thành công.
D. Các số nguyên tố đều là số lẻ.
Lời giải:
Đáp án đúng là C
Mệnh đề toán học là một khẳng định về một sự kiện trong toán học.
Do đó A, B, D đều là các mệnh đề toán học.
Ý C không là mệnh đề toán học.
Bài 42 trang 16 SBT Toán 10 Tập 1: Phủ định của mệnh đề “∀n ∈ ℕ, n2 + n là số chẵn” là:
A. “∀n ∈ ℕ, n2 + n không là số chẵn”.
B. “∃n ∈ ℕ, n2 + n không là số lẻ”.
C. “∃n ∈ ℕ, n2 + n là số lẻ”.
D. “∃n ∈ ℕ, n2 + n là số chẵn”.
Lời giải:
Đáp án đúng là C
Phủ định của mệnh đề “∀n ∈ ℕ, n2 + n là số chẵn” là mệnh đề “∃n ∈ ℕ, n2 + n không là số chẵn” hay “∃n ∈ ℕ, n2 + n là số lẻ”.
Bài 43 trang 16 SBT Toán 10 Tập 1: Cho tập hợp A = {x ∈ ℝ| – 3 ≤ x < 2}. A là tập hợp nào sau đây?
A. (– 3; 2).
B. { – 3; – 2; – 1; 0; 1}.
C. {– 3; 2}.
D. [– 3; 2).
Lời giải:
Đáp án đúng là D
Ta có A = {x ∈ ℝ| – 3 ≤ x < 2} là tập hợp gồm các số thực thỏa mãn – 3 ≤ x < 2. Do đó A = {x ∈ ℝ| – 3 ≤ x < 2} = [– 3; 2).
A. 0 và 1.
B. – 1; 0; 1 và 2.
C. 1 và 2.
D. 1.
Lời giải:
Đáp án đúng là A
Xét x + 3 < 4 + 2x
⇔ x – 2x < 4 – 3
⇔ –x < 1
⇔ x > – 1.
⇒ A = (– 1; +∞)
Xét 5x – 3 < 4x – 1
⇔ 5x – 4x < – 1 + 3
⇔ x < 2
⇒ B = (– ∞; 2)
Tập tất cả các số thực thuộc cả hai tập hợp A và B là A∩B.
Khi đó A∩B = (– 1; 2).
Ta cần tìm các số nguyên thuộc cả hai tập hợp A và B hay chính là tìm số nguyên thuộc tập A∩B .
Suy ra các số nguyên thỏa mãn điều kiện trên là 0 và 1.
Bài 45 trang 16 SBT Toán 10 Tập 1: Cho hai tập hợp E = (2; 4] và F = (4; 5). E∪F bằng:
A. (2; 5).
B. ∅.
C. [2; 5).
D. (2; 5].
Lời giải:
Đáp án đúng là A
Ta có: E = (2; 4] = {x ∈ ℝ| 2 < x ≤ 4} và F = (4; 5) = {x ∈ ℝ| 4 < x < 5}
Khi đó E∪F = {x ∈ ℝ| 2 < x ≤ 4 hoặc 4 < x < 5} = {x ∈ ℝ| 2 < x < 5} = (2; 5).
Bài 46 trang 16 SBT Toán 10 Tập 1: Cho hai tập hợp A = [–4; 3) và B = (– 2; +∞). A\B bằng:
A. [– 4; – 2);
B. {– 4; – 3; – 2}.
C. [3; +∞).
D. [– 4; – 2].
Lời giải:
Đáp án đúng là D
Ta có: A = [–4; 3) = {x ∈ ℝ| – 4 ≤ x < 3} và B = (– 2; +∞) = {x ∈ ℝ| x > – 2}
Khi đó A\B = {x ∈ ℝ| – 4 ≤ x < 3}\{x ∈ ℝ| x > – 2} = {x ∈ ℝ| – 4 ≤ x ≤ – 2} = [– 4; – 2].
a) A: “Phương trình x2 – x + 1 = 0 có nghiệm thực”;
b) B: “Hình bình hành có tâm đối xứng”.
Lời giải:
a) Mệnh đề phủ định của mệnh đề A: “Phương trình x2 – x + 1 = 0 có nghiệm thực” là ˉA: “Phương trình x2 – x + 1 = 0 vô nghiệm”.
Xét phương trình x2 – x + 1 = 0 có ∆ = (–1)2 – 4.1.1 = – 3 < 0. Suy ra phương trình vô nghiệm.
Do đó mệnh đề A sai, mệnh đề ˉA đúng.
b) Mệnh đề phủ định của mệnh đề B: “Hình bình hành có tâm đối xứng” là ˉB: “Hình bình hành không có tâm đối xứng”.
Hình bình hành là hình có tâm đối xứng với tâm đối xứng là giao điểm của hai đường chéo. Do đó mệnh đề B đúng, mệnh đề ˉB sai.
Giải SBT Toán 10 trang 17 Tập 1
Bài 48 trang 17 SBT Toán 10 Tập 1: Cho hình thang ABCD. Xét mệnh đề P ⇒ Q như sau:
Lời giải:
Mệnh đề đảo của mệnh đề P ⇒ Q là mệnh đề Q ⇒ P được phát biểu như sau: “Nếu hình thang ABCD có hai cạnh bên bằng nhau thì hình thang ABCD cân”.
Hình bính hành ABCD là một hình thang có hai cạnh bên bằng nhau tuy nhiên hai đường chéo của hình bình hành không bằng nhau. Do đó hình bình hành không là hình than cân.
Suy ra mệnh để đảo Q ⇒ P là mệnh đề sai.
Bài 49 trang 17 SBT Toán 10 Tập 1: Cho tứ giác ABCD. Xét các mệnh đề:
P: “Tứ giác ABCD là hình bình hành”, Q: “Tứ giác ABCD có các cạnh đối bằng nhau”.
Lời giải:
Mệnh đề P ⇒ Q được phát biểu như sau:
“Nếu tứ giác ABCD là hình bình hành thì tứ giác ABCD có các cạnh đối bằng nhau”.
Mệnh đề Q ⇒ P được phát biểu như sau:
“Nếu tứ giác ABCD có các cạnh đối bằng nhau thì tứ giác ABCD là hình bình hành”.
Ta có tứ giác ABCD là hình hành thì theo tính chất tứ giác ABCD có các cặp cạnh đối bằng nhau. Do đó mệnh đề P ⇒ Q đúng.
Ngược lại ta có tứ giác ABCD có các cặp cạnh đối bằng nhau thì theo dấu hiệu nhận biết tứ giác ABCD là hình hành. Do đó mệnh đề Q ⇒ P đúng.
Từ đó ta có mệnh đề tương đương P ⇔ Q được phát biểu như sau:
“Tứ giác ABCD là hình hành khi và chỉ khi tứ giác ABCD có các cặp cạnh đối bằng nhau”.
d) D: “∀n ∈ ℕ, n2 + 1 không chia hết cho 3”.
Lời giải:
a) Mệnh đề phủ định của mệnh đề A: “∀n ∈ ℕ*, n > 1n” là mệnh đề ˉA: “∃n ∈ ℕ*, n ≤ 1n”.
Vì n ∈ ℕ* nên 1 ≤ n ⇔ 1n≤nn=1≤n.
Suy ra n ≥ 1n ∀n ∈ ℕ*. Do đó mệnh đề A sai và mệnh đề ˉA đúng.
b) Mệnh đề phủ định của mệnh đề B: “∃x ∈ ℤ, 2x + 3 = 0” là mệnh đề ˉB: “∀x ∈ ℤ, 2x + 3 ≠ 0”.
Xét 2x + 3 = 0
⇔ x = −32
Mà −32∉ℤ
Do đó không tồn tại số nguyên x thỏa mãn 2x + 3 = 0.
Suy ra mệnh đề B sai và mệnh đề ˉB đúng.
c) Mệnh đề phủ định của mệnh đề C: “∃x ∈ ℚ, 4x2 – 1 = 0” là mệnh đề ˉC: “∀x ∈ ℚ, 4x2 – 1 ≠ 0”.
Xét phương trình: 4x2 – 1 = 0
⇔ 4x2 = 1
⇔ x2 = 14
⇔ [x=−12x=12
Mà −12;12∈ℚ nên tồn tại số hữu tỉ x=−12 hoặc x=12 thỏa mãn 4x2 – 1 = 0.
Do đó mệnh đề C đúng, mệnh đề ˉCsai.
d) Mệnh đề phủ định của mệnh đề D: “∀n ∈ ℕ, n2 + 1 không chia hết cho 3” là mệnh đề ˉD: “∃n ∈ ℕ, n2 + 1 chia hết cho 3”.
Ta xét các trường hợp sau của n:
TH1. n chia hết cho 3: n = 3k (k ∈ ℕ)
⇒ n2 + 1 = 9k2 + 1 không chia hết cho 3.
TH2. n chia cho 3 dư 1: n = 3k + 1 (k ∈ ℕ)
⇒ n2 + 1 = 9k2 + 6k + 1 + 1 = 9k2 + 6k + 2 không chia hết cho 3.
TH2. n chia cho 3 dư 2: n = 3k + 2 (k ∈ ℕ)
⇒ n2 + 1 = 9k2 + 12k + 4 + 1 = 9k2 + 12k + 5 không chia hết cho 3.
Suy ra n2 + 1 không chia hết cho 3 với mọi số tự nhiên n.
Do đó mệnh đề D đúng và mệnh đề ˉD sai.
a) A = {x ∈ ℝ| – 7 < x < – 4};
Lời giải:
a) A = {x ∈ ℝ| – 7 < x < – 4} = (– 7; – 4).
Ta có trục số như sau:

Khoảng (– 7; – 4) được biểu diễn bởi phần tô màu đỏ trên hình vẽ.
b) B = {x ∈ ℝ| – 3 ≤ x ≤ 1} = [– 3; 1].
Ta có trục số như sau:

Đoạn [– 3; 1] được biểu diễn bởi phần tô màu đỏ trên hình vẽ.
c) C = {x ∈ ℝ| x ≤ 0} = ( –∞; 0].
Ta có trục số như sau:

Nửa khoảng ( –∞; 0] được biểu diễn bởi phần tô màu đỏ trên hình vẽ.
d) D = {x ∈ ℝ| x > – 1} = (– 1; +∞).
Ta có trục số như sau:

Khoảng (– 1; +∞) được biểu diễn bởi phần tô màu đỏ trên hình vẽ.
Lời giải:
Ta có: A = [– 1; 2) = {x ∈ ℝ| – 1 ≤ x < 2}
B = (– ∞; 1] = {x ∈ ℝ| x ≤ 1}
Khi đó:
A ∩ B = {x ∈ ℝ| – 1 ≤ x < 2, x ≤ 1} = {x ∈ ℝ| – 1 ≤ x ≤ 1} = [– 1; 1].
A ∪ B = {x ∈ ℝ| – 1 ≤ x < 2 hoặc x ≤ 1} = {x ∈ ℝ| x < 2} = (– ∞; 2).
A \ B = {x ∈ ℝ| – 1 ≤ x < 2} \ {x ∈ ℝ| x ≤ 1} = {x ∈ ℝ| 1 < x < 2} = (1; 2).
B \ A = {x ∈ ℝ| x ≤ 1} \ {x ∈ ℝ| – 1 ≤ x < 2} = {x ∈ ℝ| x < – 1} = (– ∞; – 1).
ℝ \ B = ℝ \ {x ∈ ℝ| x ≤ 1} = {x ∈ ℝ| x > 1} = (1; +∞)
CℝA = ℝ \ {x ∈ ℝ| – 1 ≤ x < 2} = {x ∈ ℝ| x < – 1, x ≥ 2} = (– ∞; – 1) ∪ [2; +∞).
Lời giải:
Tập hợp A \ B là tập gồm những phần tử thuộc tập hợp A và không thuộc tập hợp B nghĩa là những phần tử x là nghiệm của đa thức P(x) nhưng không là nghiệm của đa thức Q(x) hay A \ B = {x ∈ ℝ| P(x) = 0 và Q(x) ≠ 0}.
Xét P(x)Q(x)=0 (*)
Điều kiện xác định là: Q(x) ≠ 0
(*) ⇔ P(x) = 0
Do đó tập hợp C bao gồm những phần tử thỏa mãn P(x) = 0 và Q(x) ≠ 0.
⇒ C = {x ∈ ℝ| P(x) = 0 và Q(x) ≠ 0}.
Vậy A = C.
Lời giải:
Để B \ A = ∅ thì B ⊂ A.
Do đó để B ⊂ A thì:
{m+1≥−1m+3≤4⇔{m≥−2m≤1⇔−2≤m≤1
Vậy với −2≤m≤1 thì B \ A = ∅.
Lời giải:
Số học sinh đăng kí tham gia ít nhất một nội dung là 40 – 19 = 21 (học sinh).
Số học sinh đăng kí tham gia cả hai nội dung là: 15 + 10 – 21 = 4 (học sinh).
Vậy có 4 học sinh đăng kí tham gia cả hai nội dung.
Lời giải:
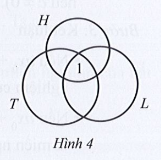
Gọi T là tập hợp học sinh đăng kí thi môn Toán; L là tập hợp học sinh đăng kí thi môn Lí; H là tập hợp học sinh đăng kí thi môn Hóa.
Dựa vào biểu đồ Venm ta có số học sinh chỉ đăng kí thi môn Toán là: 7 – 3 – 4 + 1 = 1.
Số học sinh chỉ đăng kí thi môn Lí là: 5 – 3 – 2 + 1 = 1.
Số học sinh đăng kí thi môn Toán và Lí mà không đăng kí môn Hóa là: 3 – 2 = 1.
Vậy tổng số học sinh lớp 10A đăng kí thi ba môn trên là: 1 + 1 + 2 + 6 = 10 (học sinh).
Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:
Bài 2: Tập hợp. Các phép toán trên tập hợp
Bài 1: Bất phương trình bậc nhất hai ẩn




