Giải SBT Toán 10 (Cánh diều) Bài 1: Bất phương trình bậc nhất hai ẩn

Giải Sách bài tập Toán 10 Bài 1: Bất phương trình bậc nhất hai ẩn

Giải SBT Toán 10 trang 24 Tập 1

Bài 1 trang 24 SBT Toán 10 Tập 1: Cặp số nào sau đây là nghiệm của bất phương trình – 3x + 5y ≤ 6.

A. (2; 8);

B. (– 10; – 3);

C. (3; 3);

D. (0; 2).

Lời giải:

Đáp án đúng là C

+) Thay x = 2, y = 8 vào bất phương trình – 3x + 5y ≤ 6, ta được:

– 3.2 + 5.8 ≤ 6 ⇔ 34 ≤ 6 (vô lí)

Do đó cặp số (2; 8) không là nghiệm của bất phương trình đã cho.

+) Thay x = – 10, y = – 3 vào bất phương trình – 3x + 5y ≤ 6, ta được:

– 3.(–10) + 5.(–3) ≤ 6 ⇔ 15 ≤ 6 (vô lí)

Do đó cặp số (– 10; – 3) không là nghiệm của bất phương trình đã cho.

+) Thay x = 3, y = 3 vào bất phương trình – 3x + 5y ≤ 6, ta được:

– 3.3 + 5.3 ≤ 6 ⇔ 6 ≤ 6 (luôn đúng)

Do đó cặp số (3; 3) không là nghiệm của bất phương trình đã cho.

+) Thay x = 0, y = 2 vào bất phương trình – 3x + 5y ≤ 6, ta được:

– 3.0 + 5.2 ≤ 6 ⇔ 10 ≤ 6 (vô lí)

Do đó cặp số (0; 2) không là nghiệm của bất phương trình đã cho.

Bài 2 trang 24 SBT Toán 10 Tập 1: Miền nghiệm của bất phương trình 2x – 3y > 5 là nửa mặt phẳng (không kể đường thẳng d: 2x – 3y = 5) không chứa điểm có tọa độ nào sau đây?

A. (0; 0);

B. (3; 0);

C. (1; – 2);

D. (– 3; – 4).

Lời giải:

Đáp án đúng là B

+) Thay x = 0, y = 0 vào bất phương trình 2x – 3y > 5, ta được:

2.0 – 3.0 > 5 ⇔ 0 > 5 (vô lí)

Do đó cặp số (0; 0) không thuộc miền nghiệm của bất phương trình đã cho.

+) Thay x = 3, y = 0 vào bất phương trình 2x – 3y > 5, ta được:

2.3 – 3.0 > 5 ⇔ 6 > 5 (thỏa mãn)

Do đó cặp số (0; 0) thuộc miền nghiệm của bất phương trình đã cho.

+) Thay x = 1, y = – 2 vào bất phương trình 2x – 3y > 5, ta được:

2.1 – 3.(– 2)  > 5 ⇔ 8 > 5 (thỏa mãn)

Do đó cặp số (1; – 2) thuộc miền nghiệm của bất phương trình đã cho.

+) Thay x = – 3, y = –4 vào bất phương trình 2x – 3y > 5, ta được:

2.(– 3) – 3.(– 4)  > 5 ⇔ 6 > 5 (thỏa mãn)

Do đó cặp số (– 3; – 4) thuộc miền nghiệm của bất phương trình đã cho.

Bài 3 trang 24 SBT Toán 10 Tập 1: Miền nghiệm của bất phương trình x – 2y < 4 được xác định bởi miền nào (nửa mặt phẳng không bị gạch và không kể d) sau đây?

A.

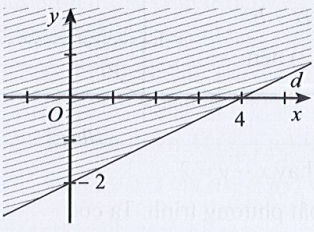
B.

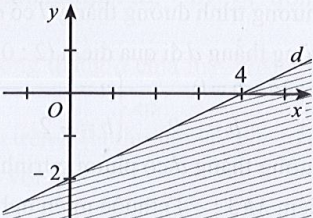
C.

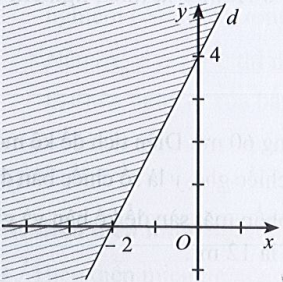
D.

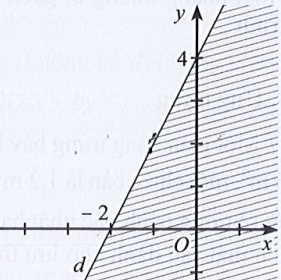
Lời giải:

Đáp án đúng là B

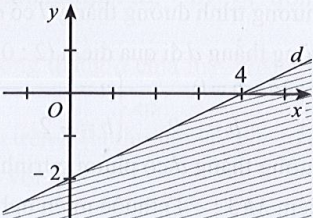
Phương trình đường thẳng d có dạng: x – 2y = 4.

Đường thẳng d cắt hai trục tọa độ Ox, Oy lần lượt tại hai điểm có tọa độ (4; 0) và (0; – 2).

Ta có: 0 – 2.0 = 0 < 4 (luôn đúng). Do đó miền nghiệm của bất phương trình chứa điểm (0; 0) và không chứa đường thẳng d.

Khi đó miền nghiệm là nửa mặt phẳng không bị gạch và không kể d được thể hiện trong hình vẽ sau:

Giải SBT Toán 10 trang 25 Tập 1

Bài 4 trang 25 SBT Toán 10 Tập 1: Nửa mặt phẳng không bị gạch (không kể d) ở Hình 3 là miền nghiệm của bất phương trình nào sau đây?

A. 3x + y < 3;

B. x + 3y > 3;

C. x + 3y < 3;

D. 3x + y > 3.

Lời giải:

Đáp án đúng là D

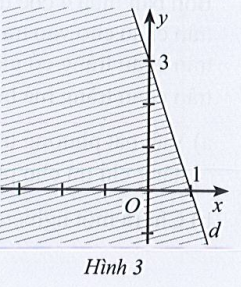
Gọi đường thẳng d có dạng: y = ax + b (a ≠ 0)

Đường thẳng d cắt trục Ox tại điểm có tọa độ (1; 0), thay tọa độ này vào phương trình đường thẳng d ta được: 0 = a.1+ b ⇔ a + b = 0 (1).

Đường thẳng d cắt trục Oy tại điểm có tọa độ (0; 3), thay tọa độ này vào phương trình đường thẳng d ta được: 3 = a.0 + b ⇔ b = 3.

Thay b = 3 vào (1) ta được: a + 3 = 0 ⇔ a = – 3 (thỏa mãn).

Khi đó phương trình đường thẳng d là: y = – 3x + 3 hay 3x + y = 3.

Ta có: 3.0 + 0 = 0 < 3 và dựa vào hình vẽ ta thấy điểm (0; 0) không thuộc vào miền nghiệm của bất phương trình đã cho và không kể đường thẳng d nên 3x + y > 3.

Vậy nửa mặt phẳng không bị gạch (không kể d) ở Hình 3 biểu diền miền nghiệm của bất phương trình 3x + y > 3.

Bài 5 trang 25 SBT Toán 10 Tập 1: Nửa mặt phẳng không bị gạch (kể cả d) ở Hình 4 là miền nghiệm của bất phương trình nào sau đây?

A. 2x – y ≤ 0;

B. 2x – y ≥ 0;

C. x – 2y ≥ 0;

D. x – 2y ≤ 0.

Lời giải:

Đáp án đúng là A

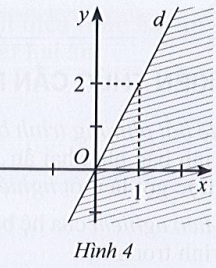
Gọi đường thẳng d có dạng: y = ax + b (a ≠ 0)

Đường thẳng d đi qua gốc tọa độ (0; 0), thay tọa độ này vào phương trình đường thẳng d ta được: 0 = a.0 + b ⇔ b = 0 (1).

Đường thẳng d đi qua điểm có tọa độ (1; 2), thay tọa độ này vào phương trình đường thẳng d ta được: 2 = a.1 + b ⇔ a + b = 2.

Mà b = 0 nên a + 0 = 2 ⇔ a = 2 (thỏa mãn).

Khi đó phương trình đường thẳng d là: y = 2x hay 2x – y = 0.

Ta có: 2.0 – 2 = – 2 < 0 và dựa vào hình vẽ ta thấy điểm (0; 2) thuộc vào miền nghiệm của bất phương trình đã cho và kể cả đường thẳng d nên 2x – y ≤ 0.

Vậy nửa mặt phẳng không bị gạch (kể cả d) ở Hình 4 biểu diền miền nghiệm của bất phương trình 2x – y ≤ 0.

Bài 6 trang 25 SBT Toán 10 Tập 1: Cặp số nào sau đây là nghiệm của bất phương trình – 5x + 2y > 10?

a) (– 2; 1);

b) (1; 5);

c) (0; 5).

Lời giải:

a) Thay x = – 2, y = 1 vào bất phương trình – 5x + 2y > 10, ta được:

– 5.(– 2) + 2.1 > 10 ⇔ 12 > 10 (luôn đúng)

Do đó cặp số (– 2; 1) là nghiệm của bất phương trình đã cho.

b) Thay x = 1, y = 5 vào bất phương trình – 5x + 2y > 10, ta được:

– 5.1 + 2.5 > 10 ⇔ 5 > 10 (vô lí)

Do đó cặp số (1; 5) không là nghiệm của bất phương trình đã cho.

c) Thay x = 0, y = 5 vào bất phương trình – 5x + 2y > 10, ta được:

– 5.0 + 2.5 > 10 ⇔ 10 > 10 (vô lí)

Do đó cặp số (0; 5) không là nghiệm của bất phương trình đã cho.

Vậy chỉ có cặp số (– 2; 1) là nghiệm của bất phương trình đã cho.

Bài 7 trang 25 SBT Toán 10 Tập 1: Biểu diễn miền nghiệm của mỗi bất phương trình sau:

a) 3x + 5y < 15;

b) x – 2y ≥ 6;

c) y > – x + 3;

d) y ≤ 4 – 2x.

Lời giải:

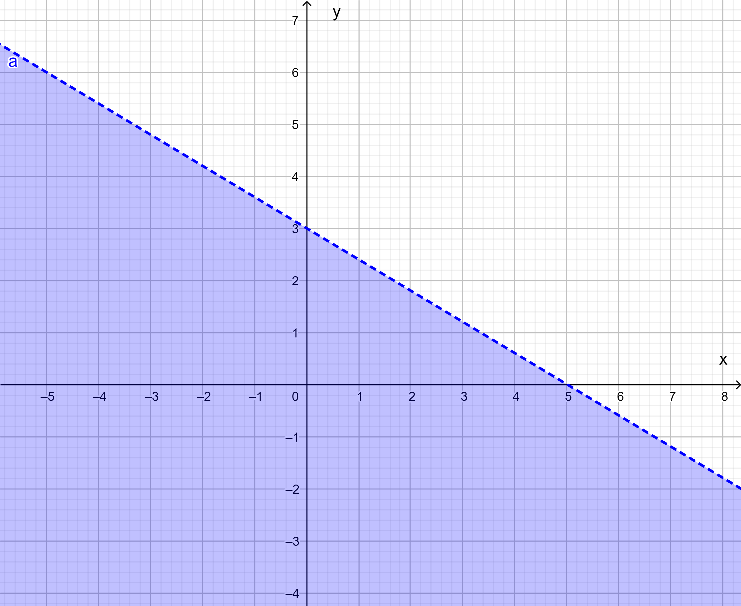
a) Biểu diễn miền nghiệm của bất phương trình 3x + 5y < 15 gồm các bước sau:

+) Vẽ đường thẳng d: 3x + 5y = 15:

Đường thẳng d đi qua hai điểm (0; 3) và (5; 0).

+) Lấy điểm O(0; 0), ta có: 3.0 + 5.0 = 0 < 15. 

Vậy miền nghiệm của bất phương trình đã cho là nửa mặt phẳng chứa điểm O(0; 0) và không kể đường thẳng d là nửa mặt phẳng tô màu trong hình sau:

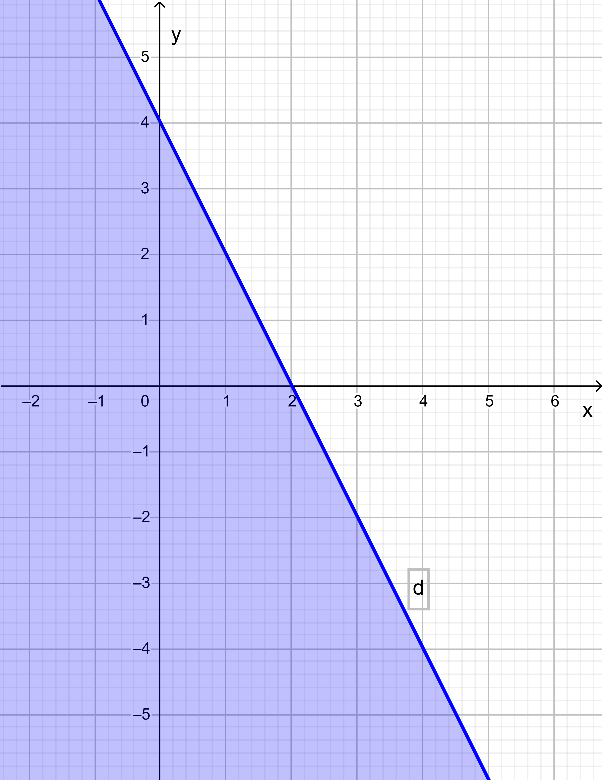
b) Biểu diễn miền nghiệm của bất phương trình x – 2y ≥ 6 gồm các bước sau:

+) Vẽ đường thẳng d: x – 2y = 6:

Đường thẳng d đi qua hai điểm (0; – 3) và (6; 0).

+) Lấy điểm O(0; 0), ta có: 0 – 2.0 = 0 < 6. 

Vậy miền nghiệm của bất phương trình đã cho là nửa mặt phẳng không chứa điểm O(0; 0) và kể cả đường thẳng d là nửa mặt phẳng tô màu trong hình sau:

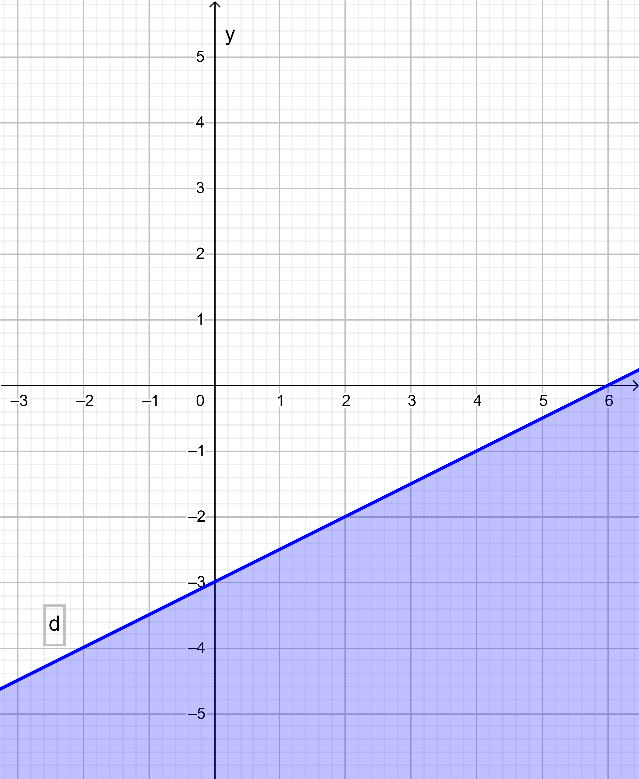
 c) Biểu diễn miền nghiệm của bất phương trình y > – x + 3 hay x + y > 3 gồm các bước sau:

+) Vẽ đường thẳng d: x + y = 3:

Đường thẳng d đi qua hai điểm (0; 3) và (3; 0).

+) Lấy điểm O(0; 0), ta có: 0 + 0 = 0 < 3. 

Vậy miền nghiệm của bất phương trình đã cho là nửa mặt phẳng không chứa điểm O(0; 0) và không kể đường thẳng d là nửa mặt phẳng tô màu trong hình sau:

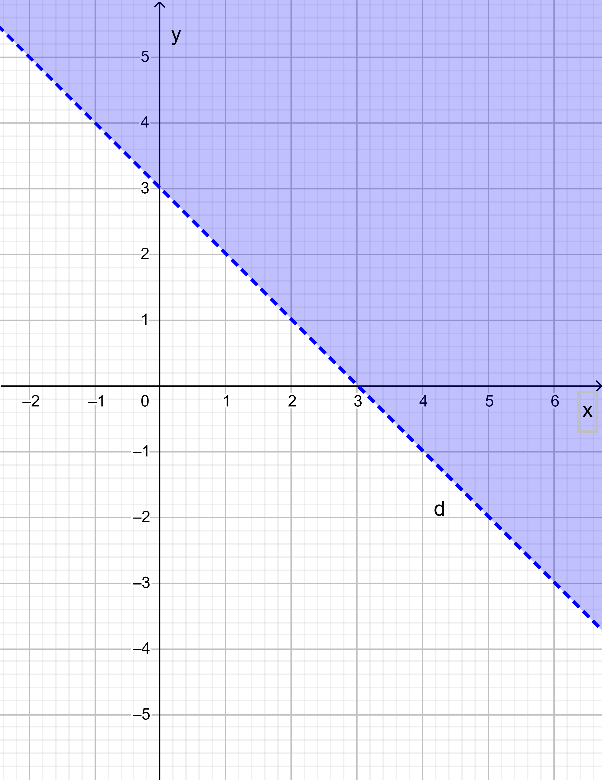
d) Biểu diễn miền nghiệm của bất phương trình y ≤ 4 – 2x hay 2x + y ≤ 4 gồm các bước sau:

+) Vẽ đường thẳng d: 2x + y = 4:

Đường thẳng d đi qua hai điểm (2; 0) và (0; 4).

+) Lấy điểm O(0; 0), ta có: 2.0 + 0 = 0 ≤ 4 . 

Vậy miền nghiệm của bất phương trình đã cho là nửa mặt phẳng chứa điểm O(0; 0) và kể cả đường thẳng d là nửa mặt phẳng tô màu trong hình sau:

Bài 8 trang 25 SBT Toán 10 Tập 1: Nửa mặt phẳng không bị gạch (không kể d) ở mỗi Hình 5a, 5b, 5c là miền nghiệm của bất phương trình nào?

Lời giải:

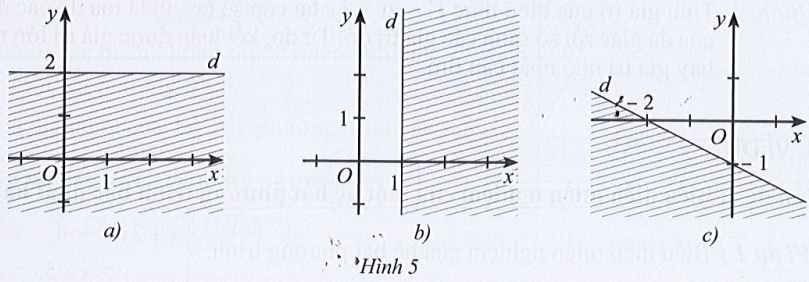
+) Hình 5b):

Đường thẳng d là đường thẳng song song với trục Ox và đi qua điểm (0; 2) nên phương trình đường thẳng d là y = 2 hay 0.x + 1.y = 2.

Lấy O(0; 0) có 0.0 + 1.0 = 0 < 2.

Quan sát trên Hình 5a) ta thấy điểm O(0; 0) không thuộc nửa mặt phẳng là miền nghiệm của bất phương trình và không kể đường thẳng d nên bất phương trình cần tìm là: y > 2.

Vậy bất phương trình có miền nghiệm được biểu diễn ở Hình 5a) là y > 2.

+) Hình 5b):

Đường thẳng d là đường thẳng song song với trục Oy và đi qua điểm (1; 0) nên phương trình đường thẳng d là x = 1 hay x + 0.y = 1.

Lấy O(0; 0) có 1.0 + 0.0 = 0 < 1.

Quan sát trên Hình 5b) ta thấy điểm O(0; 0) thuộc nửa mặt phẳng là miền nghiệm của bất phương trình và không kể đường thẳng d nên bất phương trình cần tìm là: x < 1.

Vậy bất phương trình có miền nghiệm được biểu diễn ở Hình 5b) là x < 1.

+) Hình 5c):

Gọi phương trình đường thẳng d có dạng: y = ax + b (a ≠ 0)

Đường thẳng d là đường thẳng đi qua hai điểm có tọa độ (– 2; 0) nên thay tọa độ điểm này vào phương trình d ta được: 0 = a.(– 2) + b ⇔ – 2a + b = 0 (1).

Đường thẳng d là đường thẳng đi qua hai điểm có tọa độ (0;  – 1) nên thay tọa độ điểm này vào phương trình d ta được: – 1 = a.0 + b ⇔ b =  – 1.

Thay b = 0 – 1 vào (1) ta được – 2a + (– 1) = 0 ⇔ a = $-\frac{1}{2}$.

Suy ra phương trình đường thẳng d là y = $\frac{-1}{2}$x – 1 hay $\frac{1}{2}$x + y = – 1.

Lấy O(0; 0) có $\frac{1}{2}$.0 + 0 = 0 > – 1.

Quan sát trên Hình 5c) ta thấy điểm O(0; 0) thuộc nửa mặt phẳng là miền nghiệm của bất phương trình và không kể đường thẳng d nên bất phương trình cần tìm là: $\frac{1}{2}$x + y > – 1.

Vậy bất phương trình có miền nghiệm được biểu diễn ở Hình 5c) là $\frac{1}{2}$x + y > – 1.

Giải SBT Toán 10 trang 26 Tập 1

Bài 9 trang 26 SBT Toán 10 Tập 1: Hà, Châu, Liên và Ngân cùng đi mua trà sữa. Cả bốn bạn có tất cả 185 nghìn đồng. Bốn bạn mua bốn cốc trà sữa với giá 35 nghìn đồng một cốc. Các bạn gọi thêm trân châu vào cho trà sữa. Một phần trân châu đen có giá 5 nghìn đồng, một phần trân châu trắng có giá 10 nghìn đồng. Gọi x, y lần lượt là số phần trân châu đen, trân châu trắng mà bốn bạn định mua thêm.

a) Viết bất phương trình bậc nhất hai ẩn x, y để thể hiện số tiền các bạn có đủ khả năng chi trả cho phần trân châu đen, trắng.

b) Chỉ ra một nghiệm nguyên của bất phương trình đó.

Lời giải:

a) Số tiền mua bốn cốc trà sữa là: 35.4 = 140 (nghìn đồng).

Số tiền khi thêm x phần trân châu đen là: 5x (nghìn đồng).

Số tiền khi thêm y phần trân châu trắng là: 10y (nghìn đồng).

Tổng số tiền mà bốn bạn phải trả cho 4 cốc trà sữa và phần trân châu thêm là:

5x + 10y + 140 (nghìn đồng).

Vì số tiền các bạn đem theo tất cả là 185 nghìn đồng nên 5x + 10y + 140 ≤ 185

⇔ x + 2y ≤ 9

Vậy bất phương trình bậc nhất hai ẩn x, y để thể hiện số tiền các bạn có đủ khả năng chi trả cho phần trân châu đen, trắng là x + 2y ≤ 9.

b) Chọn x = 1, y = 1 thay vào bất phương trình trên ta được:

1 + 2.1 ≤ 9 ⇔ 3 ≤ 9 (luôn đúng).

Vậy cặp (1; 1) là một nghiệm nguyên của bất phương trình đã cho.

Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài 2: Tập hợp. Các phép toán trên tập hợp

Bài ôn tập chương 1

Bài 2: Hệ bất phương trình bậc nhất hai ẩn

Bài ôn tập chương 2

Bài 1: Hàm số và đồ thị