Giải bài tập Toán lớp 8 Bài 6: Trường hợp đồng dạng thứ nhất của tam giác
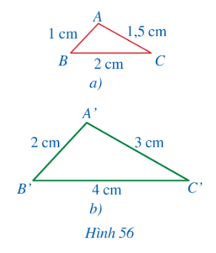
Hai tam giác A’B’C’ và ABC có đồng dạng hay không?
Lời giải:
Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:
Ta có, A'B'AB=21=2; B'C'BC=42=2; C'A'CA=31,5=2
Do đó A'B'AB=B'C'BC=C'A'CA.
Xét ∆A’B’C’ và ∆ABC có: A'B'AB=B'C'BC=C'A'CA.
Suy ra ∆A’B’C’ ᔕ ∆ABC (c.c.c).
I. Trường hợp đồng dạng thứ nhất: Cạnh-cạnh-cạnh
Hoạt động 1 trang 74 Toán 8 Tập 2: Quan sát Hình 56 và so sánh các tỉ số A'B'AB; A'C'AC; B'C'BC.
Lời giải:
Ta có A'B'AB=21=2; B'C'BC=42=2; C'A'CA=31,5=2
Do đó, A'B'AB=B'C'BC=C'A'CA.
Lời giải:
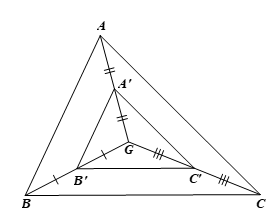
Xét ∆ABG có: A’, B’ lần lượt là trung điểm của AG; BG nên A’B’ là đường trung bình của ∆ABG
Suy ra A'B'AB=12.
Tương tự, ∆ACG có A’C’ là đường trung bình của tam giác nên A'C'AC=12.
∆CBG có C’B’ là đường trung bình của tam giác nên C'B'CB=12.
Do đó, A'B'AB=A'C'AC=C'B'CB(=12).
Suy ra ∆A’B’C’ ᔕ ∆ABC (c.c.c).
II. Áp dụng trường hợp đồng dạng thứ nhất của tam giác vào tam giác vuông
b) So sánh các tỉ số A'B'AB;B'C'BC; C'A'CA.
c) Hai tam giác A’B’C’ và ABC có đồng dạng với nhau hay không
Lời giải:
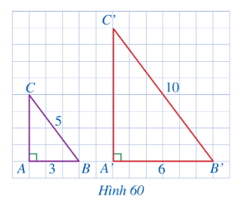
a) Xét ∆ABC vuông tại A, theo định lí Pythagore ta có:
BC2 = AB2 + AC2
Suy ra AC2 =BC2 – AB2 = 25 ‒ 9 =16.
Do đó AC = 4.
Xét ∆A’B’C’ vuông tại A’, theo định lí Pythagore ta có:
B’C’2 = A’B’2 + A’C’2
Suy ra A’C’2 =B’C’2 – A’B’2 = 100 ‒ 36 = 64
Do đó A’C’ = 8.
b) Ta có: A'B'AB=63=2; B'C'BC= 105=2; C'A'CA=84=2.
Do đó, A'B'AB=B'C'BC= C'A'CA=2
Xét ∆ABC và ∆A’B’C’ có: A'B'AB=B'C'BC= C'A'CA
Suy ra ∆A’B’C’ ᔕ ∆ABC (c.c.c).
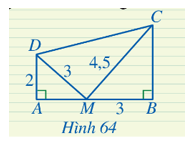
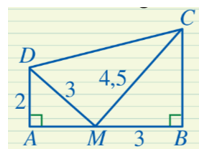
Luyện tập 2 trang 78 Toán 8 Tập 2: Cho Hình 64, chứng minh tam giác CDM vuông tại M.
Lời giải:
Ta có ADBM=23; DMMC=34,5=23nên ADBM=DMMC (=23).
Xét ∆ADM và ∆BMC có:
ˆA=ˆB=90°
Suy ra ∆ADMᔕ∆BMC.
Do đó (hai góc tương ứng)
Mà (tổng hai góc nhọn trong tam giác BCM vuông tại B bằng 90°)
Suy ra
Lại có
Nên
Do đó ∆CDM vuông tại M.
Bài tập
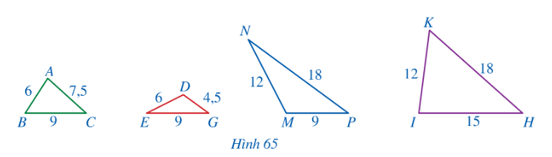
Bài 1 trang 78 Toán 8 Tập 2: Quan sát Hình 65 và chỉ ra những cặp tam giác đồng dạng:
Lời giải:
Ta có:
Do đó,
Xét ∆ABC và ∆IKHcó:
Suy ra ∆ABC ᔕ ∆IKH (c.c.c).
Tương tự, xét ∆DEG và ∆MNP có:
Suy ra ∆DEG ᔕ ∆MNP(c.c.c).
Lời giải:
Ta có:
Xét ∆ABC và ∆MNP có:
Suy ra ∆ABC ᔕ ∆MNP (c.c.c).
Do đó (các cặp góc tương ứng).
Lời giải:
∆ABC ᔕ ∆MNP theo tỉ số đồng dạng là:
Do đó
∆A’B’C’ ᔕ ∆MNP theo tỉ số đồng dạng là
Do đó
Suy ra
Tương tự ta cũng có
Do đó
Suy ra ∆A’B’C’ᔕ ∆ABC theo tỉ số đồng dạng là
Lời giải:
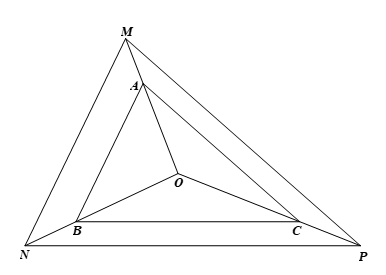
⦁ Xét tam giác OMN có: nên AB // MN (định lí Thalès đảo)
Do đó (1)
⦁ Xét tam giác OMP có: nên AC // MP (định lí Thalès đảo)
Do đó (2)
⦁ Xét tam giác ONP có: nên BC // NP (định lí Thalès đảo)
Do đó (3)
Từ (1), (2) và (3) ta có
Do đó ∆ABC ᔕ ∆MNP (c.c.c)
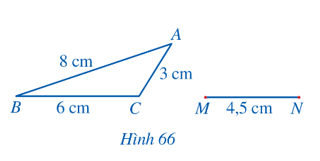
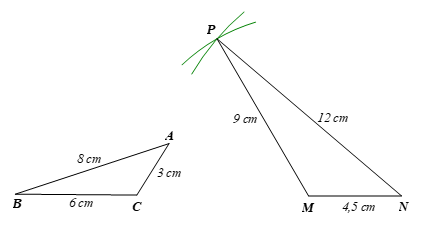
Lời giải:
Bước 1. Qua M vẽ cung tròn tâm M, bán kính là 9 cm.
Bước 2.. Qua N, vẽ cung tròn tâm N, bán kính là 12 cm.
Bước 3. Giao điểm của hai cung tròn đã vẽ là điểm P.
Ta được: MP = 9 cm; NP = 12 cm.
Ta có:
Do đó
Suy ra ∆MNP ᔕ ∆CAB nên (các cặp góc tương ứng).
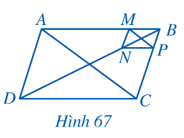
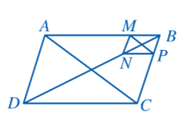
Bài 6 trang 78 Toán 8 Tập 2: Cho hình bình hành ABCD và BMNP như ở Hình 67. Chứng minh:
Lời giải:
a) Do ABCD là hình bình hành nên AD // BC và AB // CD.
Do BMNP là hình bình hành nên MN // BP và NP // BM
Do đó MN // BC // AD và NP // AB // CD.
Xét ∆ABDvới MN // AD, ta có (hệ quả của định lí Thalès) (1)
Xét ∆BDCvới NP // CD, ta có (hệ quả của định lí Thalès) (2)
Do đó
b) Xét tam giác ABC có: nên MP // AC (định lí Thalès đảo)
Suy ra (hệ quả của định lí Thalès) (3)
Vì ABCD là hình bình hành nên AD = CB; BA = CD(4)
Tư (1), (2), (3) và (4) ta có
Xem thêm các bài giải SGK Toán lớp 8 Cánh Diều hay, chi tiết khác: