Cho tam giác ABC và điểm O nằm trong tam giác. Các điểm M, N, P lần lượt thuộc tia OA, OB, OC

Bài 4 trang 78 Toán 8 Tập 2: Cho tam giác ABC và điểm O nằm trong tam giác. Các điểm M, N, P lần lượt thuộc tia OA, OB, OC sao cho $\frac{\mathrm{OA}}{\mathrm{OM}}=\frac{\mathrm{OB}}{\mathrm{ON}}=\frac{\mathrm{OC}}{\mathrm{OP}}=\frac{2}{3}.$Chứng minh ∆ABC ᔕ ∆MNP.

Trả lời

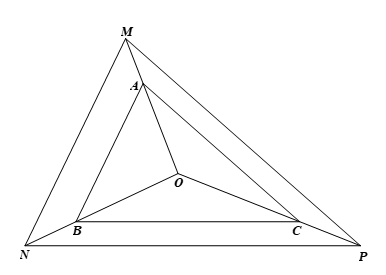
⦁ Xét tam giác OMN có: $\frac{\mathrm{OA}}{\mathrm{OM}}=\frac{\mathrm{OB}}{\mathrm{ON}}=\frac{2}{3}$ nên AB // MN (định lí Thalès đảo)

Do đó $\frac{\mathrm{OA}}{\mathrm{OM}}=\frac{\mathrm{OB}}{\mathrm{ON}}=\frac{\mathrm{AB}}{\mathrm{MN}}$ (1)

⦁ Xét tam giác OMP có: $\frac{\mathrm{OA}}{\mathrm{OM}}=\frac{\mathrm{OC}}{\mathrm{OP}}=\frac{2}{3}$ nên AC // MP (định lí Thalès đảo)

Do đó $\frac{\mathrm{OA}}{\mathrm{OM}}=\frac{\mathrm{OC}}{\mathrm{OP}}=\frac{\mathrm{AC}}{\mathrm{MP}}$ (2)

⦁ Xét tam giác ONP có: $\frac{\mathrm{OC}}{\mathrm{OP}}=\frac{\mathrm{OB}}{\mathrm{ON}}=\frac{2}{3}$ nên BC // NP (định lí Thalès đảo)

Do đó $\frac{\mathrm{OC}}{\mathrm{OP}}=\frac{\mathrm{OB}}{\mathrm{ON}}=\frac{\mathrm{BC}}{\mathrm{NP}}$ (3)

Từ (1), (2) và (3) ta có $\frac{\mathrm{AB}}{\mathrm{MN}}=\frac{\mathrm{AC}}{\mathrm{MP}}=\frac{\mathrm{BC}}{\mathrm{NP}}$

Do đó ∆ABC ᔕ ∆MNP (c.c.c)

Xem thêm các bài giải SGK Toán lớp 8 Cánh Diều hay, chi tiết khác: