Từ P và Q thẳng hàng với chân A của tháp hải đăng AB ở trên bờ biển, người ta nhìn chiều
124
05/01/2024
Bài 3 trang 81 SBT Toán 10 Tập 1: Từ P và Q thẳng hàng với chân A của tháp hải đăng AB ở trên bờ biển, người ta nhìn chiều cao AB của tháp dưới các góc ^BPA= 40° và ^BQA = 52°. Tính chiều cao của tháp hải đăng đó.
Trả lời
Ta có hình vẽ sau:
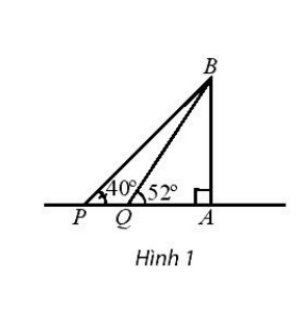
Ta có: ^BPA= 40°, ^BQA = 52°, ^BAP= 90°, PQ = 50 m.
^BQP là góc kề bù với ^BQA ⇒ ^BQP = 180° – 52° = 128°
Xét tam giác PBQ: ^PBQ+ ^BQP+ ^BPQ= 180°
⇒ ^PBQ= 180° – 128° – 40° = 12°.
Áp dụng định lí sin cho tam giác PBQ ta có:
PQsinB = BQsinP = 50sin12° ⇒ BQ = . sinP = .sin40° ≈ 154,58 m.
Xét tam giác ABQ vuông tại A: AB = BQ. sin52° = 154,58. sin52° ≈ 121,81 m.
Vậy chiều cao của tháp hải đăng khoảng 121,81 m.
Xem thêm các bài giải SBT Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Giá trị lượng giác của góc từ 0° đến 180°
Bài 2: Định lí côsin và định lí sin
Bài tập cuối chương 4
Bài 1: Khái niệm vectơ
Bài 2: Tổng và hiệu của hai vectơ
Bài 3: Tích của một số với một vectơ

