Giải SBT Toán 10 (Chân trời sáng tạo) Bài 2: Định lí côsin và định lí sin

Giải Sách bài tập Toán 10 Bài 2: Định lí côsin và định lí sin 

Giải SBT Toán 10 trang 74 Tập 1

Bài 1 trang 74 SBT Toán 10 Tập 1: Tính độ dài các cạnh chưa biết trong tam giác sau:

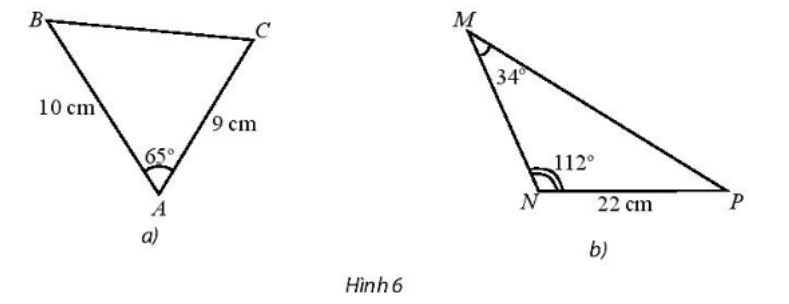
Lời giải

a) Áp dụng định lí côsin ta có:

BC² = AB² + AC² – 2.AB.AC.cos$\hat{A}$

BC² = 10² + 9² – 2.10.9.cos65°

BC ² ≈ 104,929

BC ≈ 10,24 (cm).

Vậy BC ≈ 10,24 (cm).

b) $\hat{P}$= 180° – 112° – 34° = 34°.

Ta có: $\widehat{\text{P}}$ = $\widehat{\text{M}}$ ⇒ tam giác MNP cân tại N ⇒ MN = NP = 22 (cm)

Áp dụng định lí sin ta có: $\frac{\text{MP}}{\text{sinN}}\text{ = }\frac{\text{MN}}{\text{sinP}}\text{ = }\frac{\text{NP}}{\text{sinM}}=\frac{22}{\sin 34°}$.

⇒ MP = $\frac{22}{\sin 34°}$.sin112° ≈ 36,48 (cm)

Vậy MP ≈ 36,48 cm, MN = 22 cm.

Bài 2 trang 74 SBT Toán 10 Tập 1: Cho tam giác ABC biết cạnh a = 75 cm, $\hat{B}$ = 80°, $\hat{C}$= 40°.

a) Tính các góc, các cạnh còn lại của tam giác ABC.

b) Tính bán kính đường tròn ngoại tiếp tam giác ABC.

Lời giải

a) Ta có: $\hat{A}$= 180° – 80° – 40° = 60°.

Áp dụng định lí sin ta có:

$\frac{\text{a}}{\text{sinA}}\text{ = }\frac{\text{b}}{\text{sinB}}\text{ = }\frac{\text{c}}{\text{sinC}}$ = $\frac{75}{\sin 60°}$

⇒ b = $\frac{75}{\sin 60°}$. sin80° ≈ 85,29 (cm);

⇒ c = $\frac{75}{\sin 60°}$. sin40° ≈ 55,67 (cm).

Vậy AC ≈ 85,29 cm; AB ≈ 55,67 cm và $\hat{A}$= 60°.

b) R = $\frac{\text{a}}{\text{2sinA}}$ = $\frac{75}{2.\sin 60°}$ = 25$\sqrt{3}$ (cm).

Vậy R = 25$\sqrt{3}$ cm.

Giải SBT Toán 10 trang 75 Tập 1

Bài 3 trang 75 SBT Toán 10 Tập 1: Tìm góc lớn nhất của tam giác ABC, biết a = 8, b = 12, c = 6.

Lời giải

Do b là cạnh lớn nhất nên B là góc lớn nhất.

Theo định lí côsin: b² = a² + c² – 2accosB

⇒ cosB = $\frac{{\text{a}}^2+{\text{c}}^2-{\text{b}}^2}{2\text{ac}}$ = $\frac{8^2+6^2-{12}^2}{\mathrm{2.8.6}}$

⇒ cosB = $\frac{-11}{24}$.

⇒ $\widehat{\text{B}}$ = 117°16’46’’.

Vậy góc lớn nhất của tam giác ABC là $\hat{B}$ = 117°16’46’’.

Bài 4 trang 75 SBT Toán 10 Tập 1: Tính khoảng cách giữa hai điểm P và Q của một hồ nước ( Hình 7). Cho biết từ một điểm O cách hai điểm P và Q lần lượt là 1400m và 600m người quan sát nhìn thấy một góc 76°.

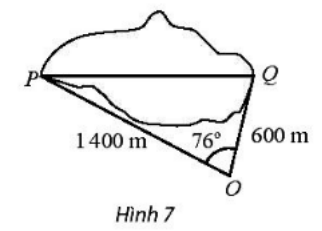
Lời giải

Áp dụng định lí côsin:

PQ² = OP² + OQ² – 2.OP.OQ.cos$\hat{O}$

PQ² = 1400² + 600² – 2.1400.600.cos76°

PQ = $\sqrt{{1400}^2+{600}^2–\mathrm{2.1400.600.}\text{cos}76°}$

PQ ≈ 1383,32 (m).

Vậy khoảng cách giữa hai điểm PQ là PQ ≈ 1383,32 (m).

Bài 5 trang 75 SBT Toán 10 Tập 1: Cho tam giác ABC với BC = a; AC = b; AB = c. Chứng minh rằng:1 + cosA = $\frac{(\text{a}+\text{b}+\text{c})(-\text{a}+\text{b}+\text{c})}{2\mathrm{bc}}$.

Lời giải

Theo định lí côsin ta có: a² = b² + c² – 2bccosA

⇒ cosA = $\frac{{\text{b}}^2+{\text{c}}^2-{\text{a}}^2}{\text{2bc}}$

Ta có:

1 + cosA = 1 + $\frac{{\text{b}}^2+{\text{c}}^2-{\text{a}}^2}{\text{2bc}}$ 

= $\frac{2\text{bc}+{\text{b}}^2+{\text{c}}^2-{\text{a}}^2}{2\text{bc}}$ 

= $\frac{{(\text{b}+\text{c})}^2-{\text{a}}^2}{2\text{bc}}$ 

= $\frac{(\text{a}+\text{b}+\text{c})(-\text{a}+\text{b}+\text{c})}{2\mathrm{bc}}$

Vậy ta có điều phải chứng minh.

Bài 6 trang 75 SBT Toán 10 Tập 1: Cho tam giác ABC có a = 24cm, b = 26cm, c = 30cm.

a) Tính diện tích tam giác ABC.

b) Tính bán kính đường tròn nội tiếp tam giác ABC.

Lời giải

a) Ta có: p = $\frac{\text{a}+\text{b}+\text{c}}{2}$ = $\frac{24+26+30}{2}$ = 40

Áp dụng công thức Heron:

S = $\sqrt{\text{p}.(\text{p}-\text{a}).(\text{p}-\text{b}).(\text{p}-\text{c})}$

S = $\sqrt{40.(40-24).(40-26).(40-30)}$

S = 80$\sqrt{14}$(cm²).

Vậy diện tích tam giác ABC là 80$\sqrt{14}$(cm²).

b) Ta có: S = p.r = 40r = 80$\sqrt{14}$

⇒ r = 2$\sqrt{14}$(cm).

Vậy bán kính đường tròn nội tiếp tam giác ABC là r = 2$\sqrt{14}$cm.

Bài 7 trang 75 SBT Toán 10 Tập 1: Cho tam giác MNP có MN = 10, MP = 20 và $\hat{M}$= 42°.

a) Tính diện tích tam giác MNP.

b) Gọi O là tâm đường tròn ngoại tiếp tam giác MNP. Tính diện tích tam giác ONP.

Lời giải

a) Diện tích tam giác MNP là:

S = $\frac{1}{2}$.MN.MP.sin$\hat{M}$= $\frac{1}{2}$.10.20.sin42° ≈ 67 (đvdt).

Vậy diện tích tam giác MNP là 67 đvdt.

b)

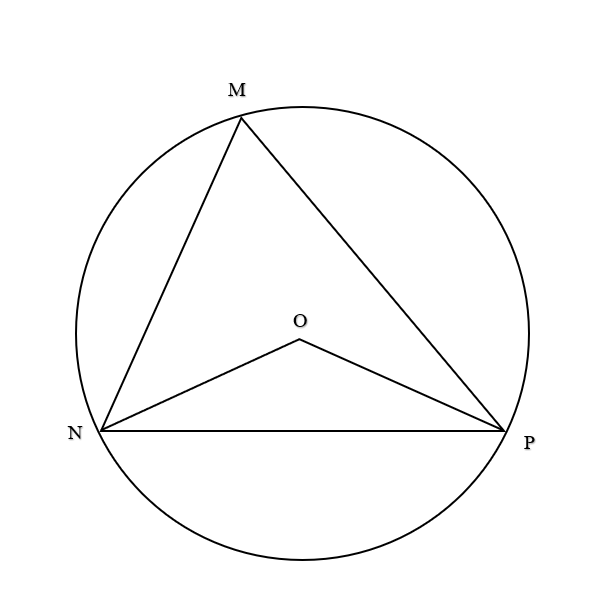
Áp dụng định lí côsin:

NP² = MP² + MN² – 2.MN.MP.cos$\hat{M}$

NP² = 10² + 20² – 2.10.20.cos42°

NP = $\sqrt{{10}^2+{20}^2–\mathrm{2.10.20.}\text{cos}42°}$

NP ≈ 14,24.

Áp dụng định lí sin trong tam giác MNP, ta có: R = ON = OP = $\frac{\text{NP}}{\text{2sin}\widehat{\text{M}}}$ ≈ $\frac{14,24}{2\sin 42°}$ ≈ 10,64

Xét đường tròn tâm O ngoại tiếp tam giác MNP:

$\widehat{\text{NMP}}$ là góc nội tiếp chắn cung NP ⇒ $\widehat{\text{NMP}}$ = $\frac{1}{2}\widehat{\text{NOP}}$ ⇒ $\widehat{\text{NOP}}$ = 42°.2 = 84°.

Suy ra S_ONP = $\frac{1}{2}$.ON.OP.sin$\widehat{\text{NOP}}$ ≈ $\frac{1}{2}$.(10,64)².sin84° ≈ 56,30 (đvdt)

Vậy diện tích tam giác ONP là 56,30 đvdt.

Bài 8 trang 75 SBT Toán 10 Tập 1: Cho tam giác ABC có trọng tâm G. Chứng minh các tam giác GBC, GAB, GAC có diện tích bằng nhau.

Lời giải

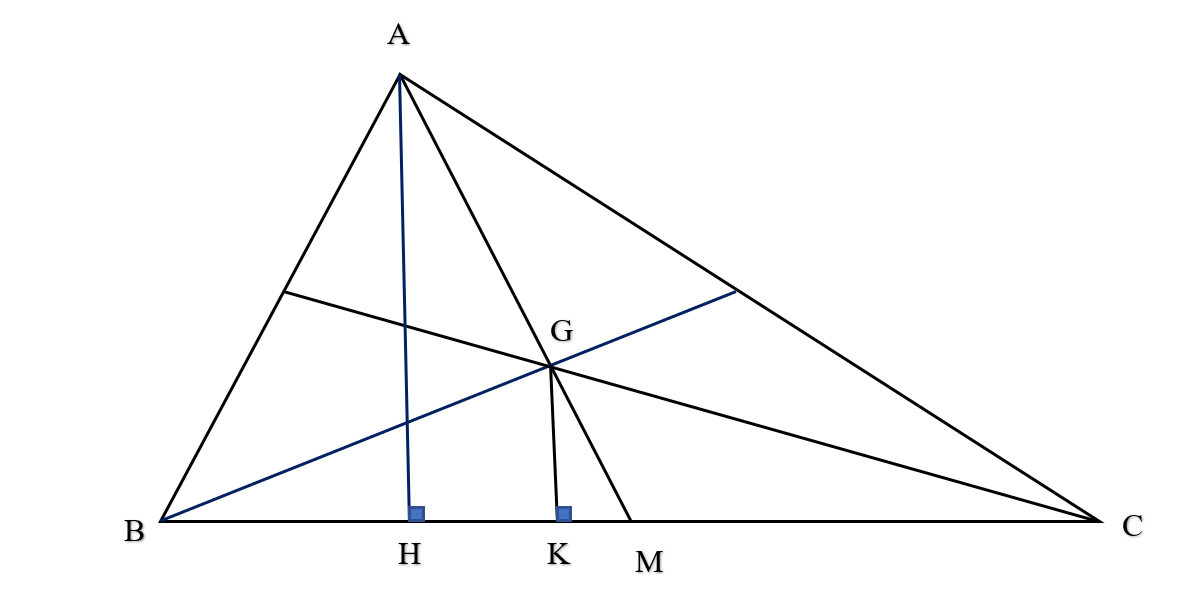
Vẽ AH và GK vuông góc với BC.

Gọi M là chân đường trung tuyến từ A hạ xuống BC. Ta có GM = AM ( tính chất đường trung tuyến của tam giác).

Xét tam giác GKM và tam giác AHM:

$\widehat{\text{AHM}}$ = $\widehat{\text{GKM}}$ = 90°

$\widehat{\text{AMH}}$ = $\widehat{\text{GMK}}$ 

⇒ tam giác GKM và tam giác AHM đồng dạng (g.g).

⇒ $\frac{\text{GM}}{\text{AM}}=\frac{\text{GK}}{\text{AH}}=\frac{1}{3}$

Có $\frac{{\text{S}}_{\text{GBC}}}{{\text{S}}_{\text{ABC}}\text{}}\text{ = }\frac{\frac{\text{1}}{\text{2}}\text{.GK.BC}}{\frac{\text{1}}{\text{2}}\text{.AH.BC}}$ = $\frac{\text{GK}}{\text{AH}}=\frac{1}{3}$.

Chứng minh tương tự ta được:

S_GBC = S_GAB = S_GAC = $\frac{1}{3}$S_ABC. ( ĐPCM).

Bài 9 trang 75 SBT Toán 10 Tập 1: Cho tam giác ABC và các điểm B’, C’ trên cạnh AB và AC. Chứng minh:

$\frac{{\text{S}}_{\text{ABC}}}{{\text{S}}_{\text{AB'C'}}}\text{ = }\frac{\text{AB.AC}}{\text{AB'.AC'}}$.

Lời giải

Ta có:

S_ABC = $\frac{1}{2}$.AB.AC.sin$\hat{A}$

S_AB’C’ = $\frac{1}{2}$.AB’.AC’.sin$\hat{A}$

⇒ $\frac{{\text{S}}_{\text{ABC}}}{{\text{S}}_{\text{AB'C'}}}$ = $\frac{\frac{\text{1}}{\text{2}}\text{.AB.AC.sin}\widehat{\text{A}}}{\frac{1}{2}\text{.AB’.AC’.sin}\widehat{\text{A}}}$

⇒ $\frac{{\text{S}}_{\text{ABC}}}{{\text{S}}_{\text{AB'C'}}}\text{ = }\frac{\text{AB.AC}}{\text{AB'.AC'}}$ (ĐPCM).

Giải SBT Toán 10 trang 76 Tập 1

Bài 10 trang 76 SBT Toán 10 Tập 1: Tính diện tích bề mặt của một miếng bánh mì kebab hình tam giác có hai cạnh lần lượt là 10cm và 12cm và góc được tạo bởi hai cạnh đó là 35°.

Lời giải

Diện tích bề mặt miếng bánh mì kebab là:

S = $\frac{1}{2}$.10.12.sin35° ≈ 34,4 (cm²).

Vậy diện tích bề mặt miếng bánh mì kebab khoảng 34,4 cm².

Xem thêm lời giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 3

Bài 1: Giá trị lượng giác của  góc từ 0° đến 180°

Bài tập cuối chương 4

Bài 1: Khái niệm vectơ

Bài 2: Tổng và hiệu của hai vectơ