Giải Sách bài tập Toán 10 Bài 2: Tổng và hiệu của hai vectơ
Giải SBT Toán 10 trang 94 Tập 1
![]()
Lời giải:
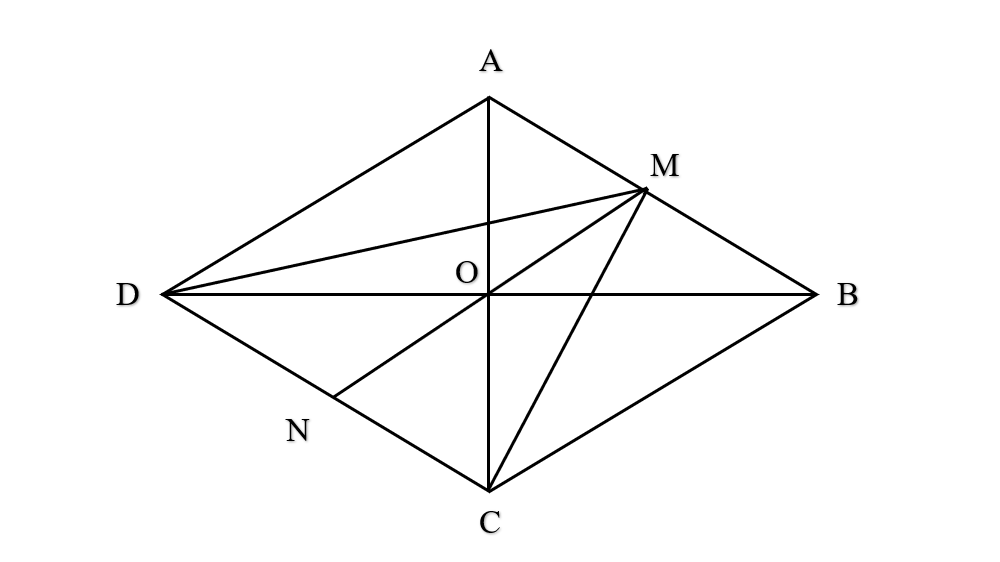
Gọi O là tâm hình thoi. O là trung điểm của AC và BD ( tính chất hình thoi).
⇒ ![]() và
và ![]()
Ta có:
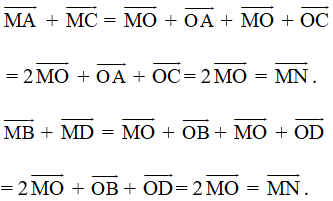
Vậy ![]()
Bài 2 trang 94 SBT Toán 10 Tập 1: Chứng minh rằng với tứ giác ABCD bất kì, ta luôn có:
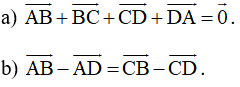
Lời giải:
a) Theo quy tắc ba điểm cộng vectơ ta có:
![]()
Như vậy: ![]()
b) Ta có:
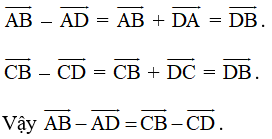
Lời giải:
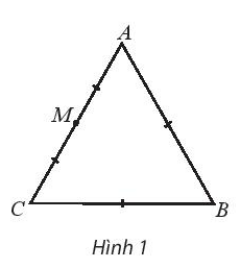
Theo quy tắc ba điểm, ta có: →AB+→BC = →AC
Tam giác ABC đều cạnh bằng a nên AC = a.
Do đó |→AB+→BC| = |→AC| = a.
Gọi M là trung điểm cạnh AC.
Ta có:
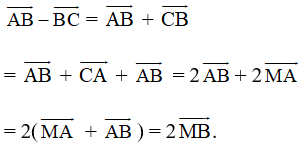
Vì MB là đường trung tuyến của tam giác đều ABC cạnh bằng a nên MB = a√32.
Do đó ![]()
Vậy ![]() và
và ![]() .
.
Bài 4 trang 94 SBT Toán 10 Tập 1: Cho hình bình hành ABCD tâm O. Chứng minh rằng:
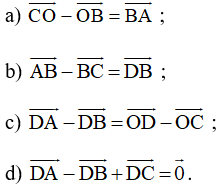
Lời giải:
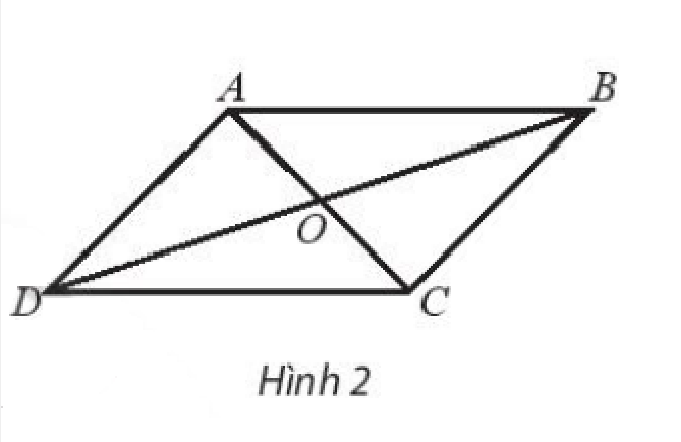
a) Vì ABCD là hình bình hành nên O là trung điểm của AC, BD.
Do đó
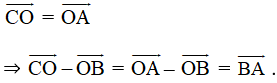
b) Vì ABCD là hình bình hành nên: →BC= →AD
Ta có:
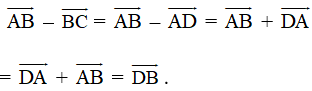
c) Ta có:
![]() và
và ![]()
Mà ta lại có ABCD là hình bình hành nên →BA = →CD.
Vậy nên →DA−→DB=→OD−→OC.
d) Theo chứng minh trên ta có:
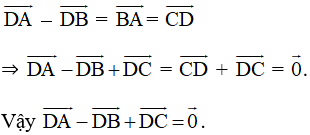
Lời giải:
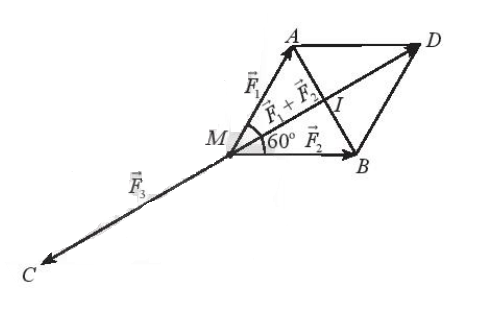
M đứng yên nên:
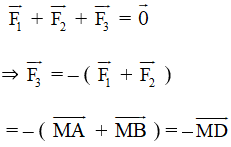
⇒ →F3 có hướng ngược với →MD và có độ lớn bằng →MD.
Dựng hình bình hành MADB.
Gọi I là giao điểm của AB và MD. Khi đó I là trung điểm của AB và MD.
Mặt khác ^AMB = 60° nên tam giác AMB đều.
Khi đó MI ⊥ AB ⇒ Tam giác AIM vuông tại I.
⇒ MI = AM.sin^MAI= 100.sin60° = 50√3 ⇒ MD = 2MI = 100√3.
Vậy độ lớn của lực →F3 bằng 100√3.
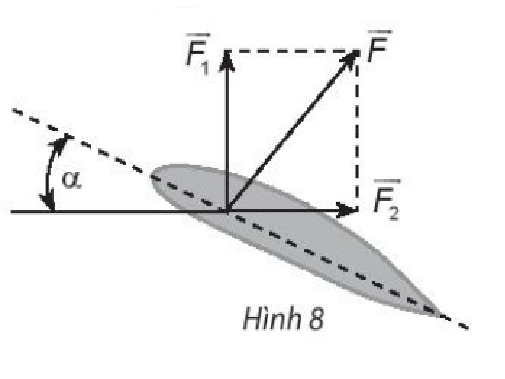
Lời giải:
Đặt tên các điểm trong hình vẽ, ta có:
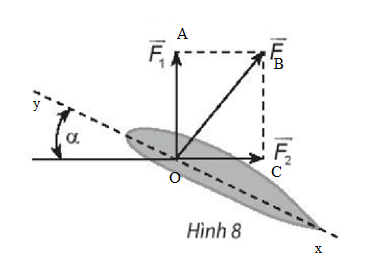
Khi đó |→F|=OB,|→F1|=OA,|→F2|=OC
Vì lực →F vuông góc với phương xy của cánh nên ^FOx=90°.
Ta có:
⇒
Xét tam giác BOC vuông tại C, có:
⇔ 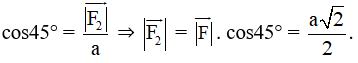
⇔ 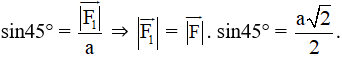
Vậy .
; .
Tìm độ dài các vectơ , .
Lời giải:
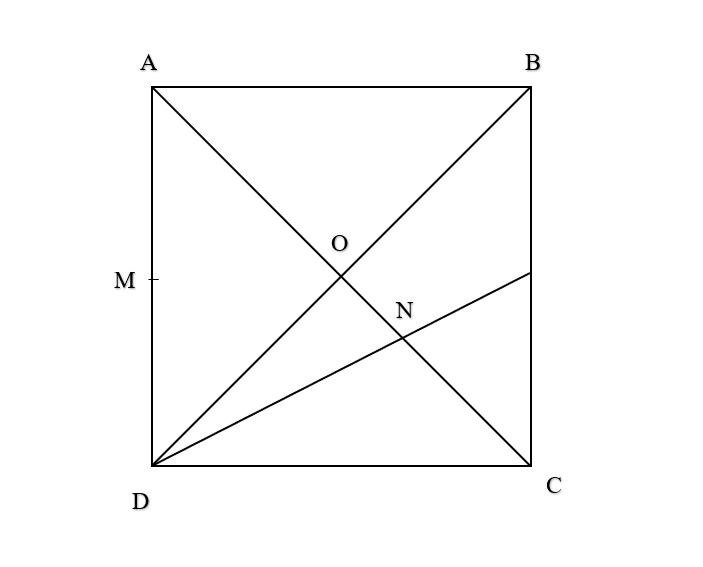
Ta có: suy ra M là trung điểm AD. Khi đó = MA = AD = .
Và suy ra N là trọng tâm tam giác BCD. Khi đó = NO = CO = CA.
Xét hình vuông ABCD, có: CA = =
Suy ra .
Xem thêm lời giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Tích của một số với một vectơ




