Giải Sách bài tập Toán 10 Bài 3: Tích của một số với một vectơ
Giải SBT Toán 10 trang 96 Tập 1
Lời giải:
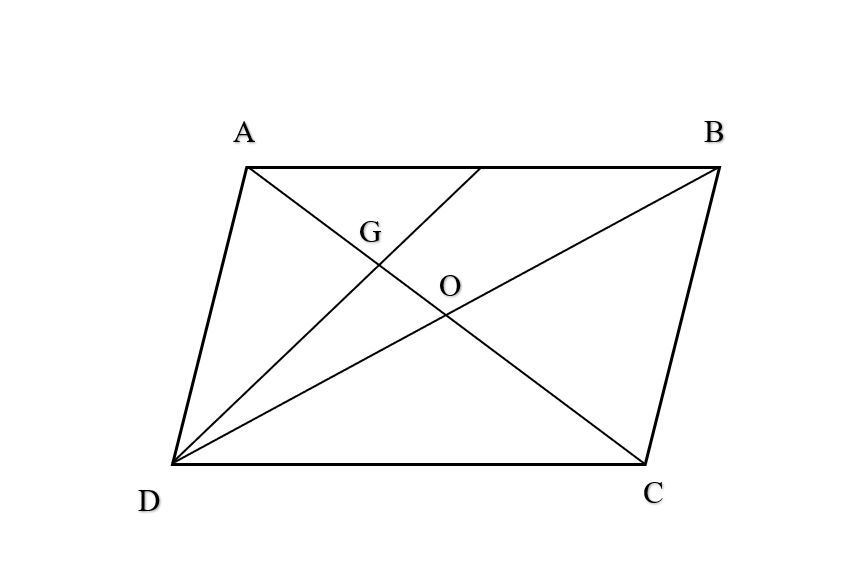
Gọi O là giao điểm của AC và BD. Khi đó 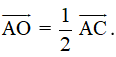
G là trọng tâm tam giác ABD 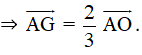
Vậy 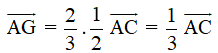 hay
hay ![]() .
.
Giải SBT Toán 10 trang 97 Tập 1
a) 2→DA+→DB+→DC=→0;
b) 2→OA+→OB+→OC=4→OD, với O là điểm tùy ý.
Lời giải:
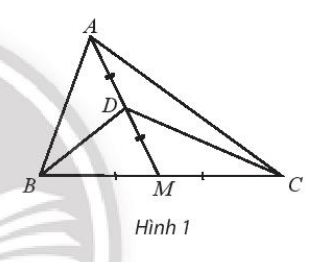
a) Vì M là trung điểm của BC nên: →DB+→DC=2→DM.
Mặt khác do D là trung điểm đoạn AM nên →DM=−→DA
Vậy nên →DB+→DC = –2→DA hay 2→DA+→DB+→DC=2→DA−2→DA=→0.
b) Ta có:
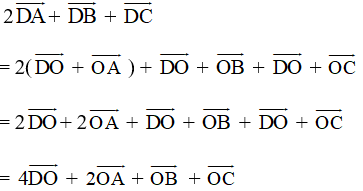
Vậy ![]() hay
hay ![]()
Bài 3 trang 97 SBT Toán 10 Tập 1: Lấy một điểm M tùy ý. Chứng minh rằng:
a) I là trung điểm của đoạn thẳng AB khi và chỉ khi →MA+→MB=2→MI.
b) G là trọng tâm của tam giác ABC khi và chỉ khi →MA+→MB+→MC=3→MG.
Lời giải:
a) Với điểm M bất kì ta có: ![]()
I là trung điểm đoạn thẳng AB nên ![]()
Khi đó: ![]()
Vậy I là trung điểm của đoạn thẳng AB khi và chỉ khi →MA+→MB=2→MI.
b) Với điểm M bất kì ta có:
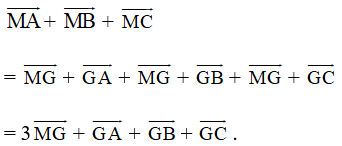
G là trọng tâm tam giác ABC nên ![]()
Khi đó 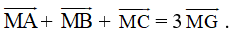
Vậy G là trọng tâm của tam giác ABC khi và chỉ khi ![]() .
.
Bài 4 trang 97 SBT Toán 10 Tập 1: Cho hai điểm phân biệt A và B. Tìm điểm K sao cho 3→KA+2→KB=→0.
Lời giải:
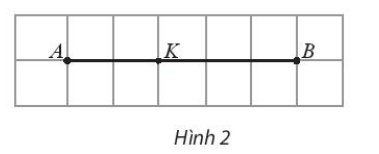
Vì 3→KA+2→KB=→0 nên 3→KA=-2→KB
Suy ra
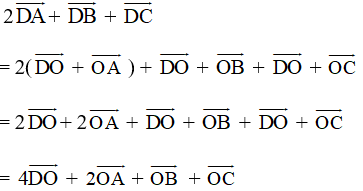
Do đó 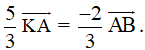
Nên 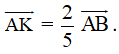
Vậy K nằm giữa A và B sao cho AK = 25AB.
Lời giải:
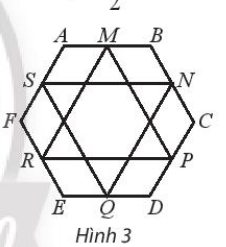
MN là đường trung bình của tam giác ABC nên ta có: →MN=12→AC.
Tương tự ta có: 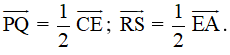
Suy ra
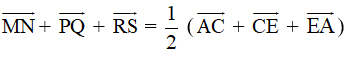
Vậy ![]()
Gọi G là trọng tâm tam giác MPR ta có: ![]()
Ta lại có:
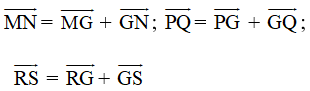
Suy ra
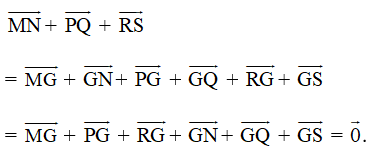
Mà
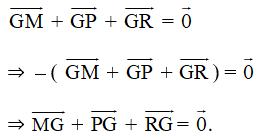
Do đó ![]()
Suy ra G là trọng tâm của tam giác NQS.
Như vậy hai tam giác MPR và NQS có cùng trọng tâm.
Lời giải:
Máy bay B bay cùng hướng và có tốc độ chỉ bằng một nửa máy A nên vectơ vận tốc của máy bay B là: →b=12→a.
Xem thêm lời giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Tổng và hiệu của hai vectơ




