Trong mặt phẳng toạ độ Oxy cho hai điểm A(1; 4) và C(9; 2) là hai đỉnh của hình vuông ABCD. Tìm toạ độ

Bài 4.35 trang 65 SBT Toán 10 Tập 1:

Trong mặt phẳng toạ độ Oxy cho hai điểm A(1; 4) và C(9; 2) là hai đỉnh của hình vuông ABCD. Tìm toạ độ các đỉnh B, D, biết rằng tung độ của B là một số âm.

Trả lời

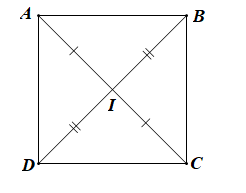
Gọi I là giao điểm của AC và BD

Vì ABCD là hình vuông nên ta có: I là trung điểm của AC; AC = BD và AC ⊥ BD tại I.

• I là trung điểm của AC nên:

$\left\{\begin{array}{l}{x}_I=\frac{1+9}{2}=5\\ y_I=\frac{4+2}{2}=3\end{array}\right.$Þ I(5; 3)

Giả sử B(x; y) (y < 0) và D(a; b)

Vì I là trung điểm của BD nên ta có:

$\left\{\begin{array}{l}5=\frac{x+a}{2}\\ 3=\frac{y+b}{2}\end{array}\right.\Rightarrow \left\{\begin{array}{l}a=10-x\\ b=6-y\end{array}\right.$ $\Rightarrow$ D(10 – x; 6 – y)

Với A(1; 4); C(9; 2); B(x; y) và D(10 – x; 6 – y) ta có:

$\overrightarrow{AC}=\left(8;-2\right)$ và $\overrightarrow{BD}=\left(10-2x;6-2y\right)$

• AC ⊥ BD $\iff \overrightarrow{AC}\perp \overrightarrow{BD}\iff \overrightarrow{AC}.\overrightarrow{BD}=0$

$\Rightarrow$ 8.(10 – 2x) + (–2).(6 – 2y) = 0

$\Rightarrow$ 80 – 16x – 12 + 4y = 0

$\Rightarrow$ 4y = 16x – 68

$\Rightarrow$ y = 4x – 17 (với y < 0)

• AC = BD $\Rightarrow$ AC² = BD²

$\Rightarrow$ 8² + (–2)² = (10 – 2x)² + (6 – 2y)²

$\Rightarrow$ 64 + 4 = (10 – 2x)² + [6 – 2(4x – 17)]²

$\Rightarrow$ (10 – 2x)² + (6 – 8x + 34)² = 68

$\Rightarrow$ (10 – 2x)² + (40 – 8x)² = 68

$\Rightarrow$ 4.(x – 5)² + 64.(x – 5)² = 68

$\Rightarrow$ (x – 5)² = 1

$\iff \left[\begin{array}{l}x-5=1\\ x-5=-1\end{array}\right.$

$\iff \left[\begin{array}{l}x=6\\ x=4\end{array}\right.$

Với x = 6 ta có y = 4.6 – 17 = 7 (không thỏa mãn y < 0)

Với x = 4 ta có y = 4.4 – 17 = –1 (thỏa mãn y < 0)

Khi đó ta có điểm B(4; –1)

Mà D(10 – x; 6 – y) nên D(6; 7).

Vậy B(4; –1) và D(6; 7).

Xem thêm các bài giải SBT Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 9: Tích của một vectơ với một số

Bài 10: Vectơ trong mặt phẳng tọa độ

Bài 11: Tích vô hướng của hai vectơ

Bài tập cuối chương 4

Bài 12: Số gần đúng và sai số

Bài 13: Các số đặc trưng đo xu thế trung tâm