Giải Sách bài tập Toán 10 Bài 10: Vectơ trong mặt phẳng tọa độ
Giải SBT Toán 10 trang 58 Tập 1
Lời giải:
Cách 1:
Gọi A(xA; yA); B(xB; yB) và C(xC; yC) là tọa độ ba đỉnh của tam giác ABC.
Ta có:
+) M(4; 0) là trung điểm của BC nên {4=xB+xC20=yB+yC2
⇒{xB+xC=8yB+yC=0 (1)
+) N(5; 2) là trung điểm của CA nên {5=xA+xC22=yA+yC2
⇒{xA+xC=10yA+yC=4⇔{xC=10−xAyC=4−yA (2)
+) P(2; 3) là trung điểm của AB nên {2=xA+xB23=yA+yB2
⇒{xA+xB=4yA+yB=6⇔{xB=4−xAyB=6−yA (3)
Thay (2) và (3) vào (1) ta được:
{(4−xA)+(10−xA)=8(6−yA)+(4−yA)=0⇔{14−2xA=810−2yA=0
⇔{xA=3yA=5 ⇒ A(3; 5)
Khi đó {xB=4−3=1yB=6−5=1 ⇒ B(1; 1)
{xC=10−3=7yC=4−5=−1⇒ C(7; –1)
Vậy A(3; 5), B(1; 1) và C(7; –1).
Cách 2:
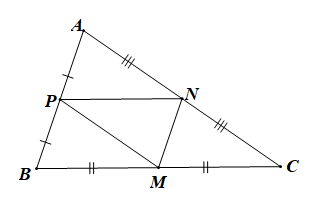
Do M, N, P lần lượt là trung điểm của BC, CA, AB
Nên MN, NP, PM là các đường trung bình của tam giác ABC.
⇒ MN // AB, NP // BC, MP // AC.
+) Do MN // BM và NP // BM nên tứ giác MNPB là hình bình hành
⇒→MB=→NP
Gọi B(xB; yB) và có M(4; 0), N(5; 2) và P(2, 3).
⇒→MB=(xB−4;yB) và →NP=(2−5;3−2)=(−3;1)
Khi đó →MB=→NP⇔{xB−4=−3yB=1⇔{xB=1yB=1 Þ B(1; 1)
Tương tự ta cũng có A(3; 5) và C(7; –1).
Vậy A(3; 5), B(1; 1) và C(7; –1).
a) Tính độ dài các đoạn thẳng AB, BC và CA. Từ đó suy ra tam giác ABC là một tam giác vuông cân.
b) Tìm toạ độ của điểm D sao cho tứ giác ABDC là một hình vuông.
Lời giải:
a) Với A(2;–1), B(1; 4) và C(7; 0) ta có:
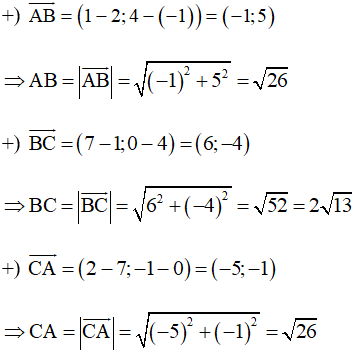
Do đó AB = CA (=√26)
Nên tam giác ABC cân tại A (1)
Mặt khác: BC2=(2√13)2=52
Và AB2+AC2=(√26)2+(√26)2=52
⇒ BC2 = AB2 + AC2
Theo định lí Pythagoras đảo thì tam giác ABC vuông tại A (2)
Từ (1) và (2) suy ra tam giác ABC vuông cân tại A với AB=AC=√26;BC=2√13.
b)
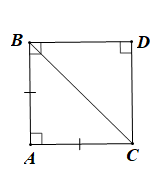
Vì ABC là tam giác vuông cân
Nên để ABDC là hình vuông thì tứ giác ABDC là hình bình hành
⇔→CA=→DB
Gọi D(xD; yD) và có A(2;–1), B(1; 4), C(7; 0).
⇒→CA=(−5;−1)và →DB=(1−xD;4−yD)
Do đó →CA=→DB⇔{−5=1−xD−1=4−yD
⇔{xD=6yD=5 ⇒ D(6; 5).
Vậy tọa độ điểm D cần tìm là D(6; 5).
Bài 4.24 trang 58 SBT Toán 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho hai điểm M(–2; 1) và N(4; 5).
a) Tìm toạ độ của điểm P thuộc Ox sao cho PM = PN.
b) Tìm toạ độ của điểm Q sao cho →MQ=2→PN.
c) Tìm toạ độ của điểm R thoả mãn →RM+2→RN=→0. Từ đó suy ra P, Q, R thẳng hàng.
Lời giải:
a) Gọi P(a; 0) là điểm thuộc tia Ox.
Với M(–2; 1) và N(4; 5) ta có:
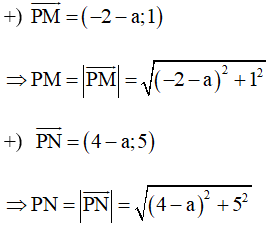
Do đó PM = PN ⇔√(−2−a)2+12=√(4−a)2+52
⇒ (–2 – a)2 + 12 = (4 – a)2 + 52
⇒ 4 + 4a + a2 + 1 = 16 – 8a + a2 + 25
⇒ 12a = 36
⇒ a = 3.
Vậy P(3; 0).
b) Giả sử điểm Q có tọa độ là Q(x; y).
Với M(–2; 1), N(4; 5) và P(3; 0) ta có:
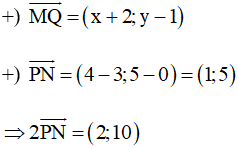
Do đó →MQ=2→PN⇔{x+2=2y−1=10
⇔{x=0y=11 ⇒ Q(0; 11).
Vậy Q(0; 11).
c) Giả sử R(x0; y0) là điểm cần tìm.
Với M(–2; 1) và N(4; 5) ta có:
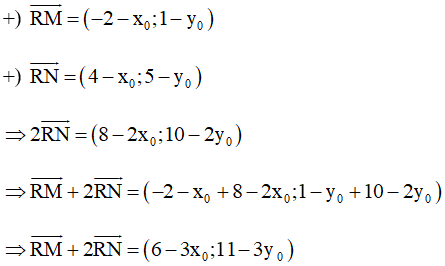
Do đó
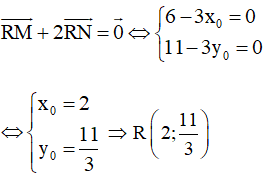
+) Ta xét ba điểm: P(3; 0), Q(0; 11) và R(2;113)
⇒→PQ=(−3;11)và →QR=(2;113−11)=(2;−223)
Có: −32=11−223 nên hai vectơ →PQ và →QR cùng phương
Do đó P, Q, R thẳng hàng
Vậy ba điểm P, Q, R thẳng hàng.
Giải SBT Toán 10 trang 59, 60 Tập 1
Bài 4.25 trang 59 SBT Toán 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho hai điểm M(–3; 2) và N(2; 7).
a) Tìm toạ độ của điểm P thuộc trục tung sao cho M, N, P thẳng hàng.
b) Tìm toạ độ của điểm Q đối xứng với N qua Oy.
c) Tìm toạ độ của điểm R đối xứng với M qua trục hoành.
Lời giải:
a) Giả sử P(0; yP) là điểm thuộc trục tung.
Với M(–3; 2) và N(2; 7) ta có:
→MP=(3;yP−2) và →NP=(−2;yP−7)
Ba điểm M, N, P thẳng hàng
⇔→MP và →NP cùng phương
⇔3−2=yP−2yP−7 (với yP ≠ 7)
⇒ 3.(yP – 7) = –2.(yP – 2)
⇒ 3.yP – 21 = –2yP + 4
⇒ 3.yP + 2yP = 4 + 21
⇒ 5.yP = 25
⇒ yP = 5 (thỏa mãn)
Vậy P(0; 5).
b)
Vì Q đối xứng với N(2; 7) qua Oy nên:
+ Hoành độ của điểm Q là số đối của hoành độ điểm N;
+ Tung độ của điểm Q bằng với tung độ của điểm N.
Do đó Q(–2; 7).
Vậy Q(–2; 7).
c)
Vì R đối xứng với M(–3; 2) qua trục hoành nên:
+ Hoành độ của điểm R bằng hoành độ điểm M;
+ Tung độ của điểm R bằng số đối của tung độ điểm M.
Do đó R(–3; –2).
Vậy R(–3; –2).
Bài 4.26 trang 60 SBT Toán 10 Tập 1:
Trong mặt phẳng toạ độ Oxy cho hai điểm C(1; 6) và D(11; 2).
a) Tìm toạ độ của điểm E thuộc trục tung sao cho vectơ →EC+→ED có độ dài ngắn nhất.
b) Tìm toạ độ của điểm F thuộc trục hoành sao cho |2→FC+3→FD| đạt giá trị nhỏ nhất.
c) Tìm tập hợp các điểm M sao cho |→MC+→MD|=CD.
Lời giải:
a) Giả sử E(0; yE) là điểm thuộc trục tung.
Với C(1; 6) và D(11; 2) ta có:
→EC=(1;6−yE) và →ED=(11;2−yE)
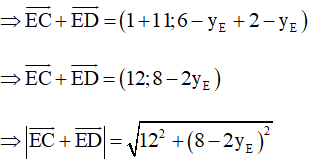
Vì (8 – 2yE)2 ≥ 0 ∀ yE
Nên 122 + (8 – 2yE)2 ≥ 122 ∀ yE
Hay √122+(8−2yE)2≥12 ∀ yE
⇒|→EC+→ED|≥12 ∀ yE
Do đó độ dài của vectơ →EC+→ED nhỏ nhất bằng 12
Dấu “=’ xảy ra ⇒ 8 – 2yE = 0
⇒ yE = 4
Vậy với E(0; 4) thì vectơ →EC+→ED có độ dài ngắn nhất.
b) Giả sử F(a; 0) thuộc trục hoành.
Với C(1; 6) và D(11; 2) ta có:
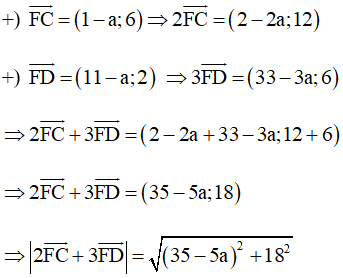
Vì (35 – 5a)2 ≥ 0 ∀a
Nên (35 – 5a)2 + 182 ≥ 182 ∀a
Hay √(35−5a)2+182 ∀a
⇒|2→FC+3→FD|≥18 ∀a
Do đó độ dài của vectơ 2→FC+3→FD nhỏ nhất bằng 18
Dấu “=’ xảy ra ⇒ 35 – 5a = 0
⇒ a = 7
Vậy với F(7; 0) thì |2→FC+3→FD| đạt giá trị nhỏ nhất.
c) Giả sử M(x ; y) là tọa độ điểm thỏa mãn |→MC+→MD|=CD.
Với C(1; 6) và D(11; 2) ta có:
+) →CD=(10;−4)
⇒CD=|→CD|=√102+(−4)2=√116=2√29
Gọi I là trung điểm của CD, khi đó ta có:
• Tọa độ của I là: {xI=1+112=6yI=6+22=4 Þ I(6; 4).
• →MC+→MD=2→MI
⇒|→MC+→MD|=|2→MI|=2.MI
Ta có
|→MC+→MD|=CD⇔2MI=CD
⇔IM=CD2=2√292=√29.
Do đó tập hợp điểm M là đường tròn tâm I(6; 4) và bán kính R=√29.
Giải SBT Toán 10 trang 61, 62 Tập 1
Bài 4.27 trang 61 SBT Toán 10 Tập 1:
Trong mặt phẳng toạ độ Oxy cho ba điểm A(1; 2), B(3; 4) và C(2; –1).
a) Chứng minh rằng A, B, C là ba đỉnh của một tam giác. Tìm toạ độ trọng tâm của tam giác đó.
b) Tìm toạ độ tâm I của đường tròn ngoại tiếp và trực tâm H của tam giác ABC.
Lời giải:
a) Với ba điểm A(1; 2), B(3; 4) và C(2; –1) ta có:
+) →AB=(2;2)
+) →AC=(1;−3)
Do 21≠2−3 nên hai vectơ →AB và →AC không cùng phương
Do đó ba điểm A, B, C không thẳng hàng nên tạo thành một tam giác.
Gọi G(x; y) là tọa độ trọng tâm của tam giác ABC
⇒{x=1+3+23=2y=2+4+(−1)3=53 ⇒G(2;53)
Vậy ⇒G(2;53)
b) * Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABC.
Gọi I(a; b) là tọa độ tâm đường tròn ngoại tiếp tam giác ABC.
Khi đó IA = IB = IC.
Với ba điểm A(1; 2), B(3; 4) và C(2; –1) ta có:
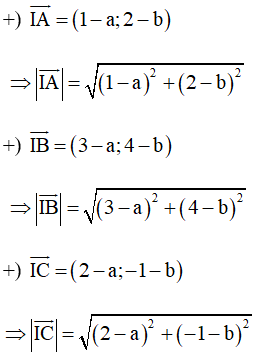
Do đó IA = IB = IC ⇒ IA2 = IB2 = IC2
⇒ (1 – a)2 + (2 – b)2 = (3 – a)2 + (4 – b)2 = (2 – a)2 + (–1 – b)2
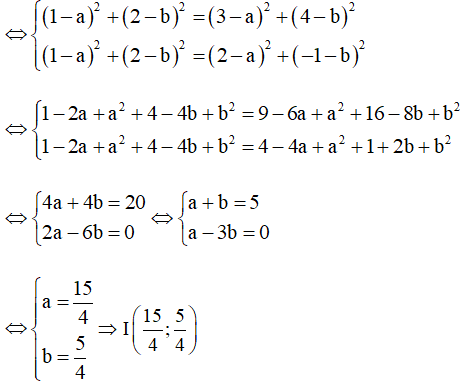
* Tìm tọa độ trực tâm H của tam giác ABC.
Gọi H(x0; y0) là tọa độ trực tâm của tam giác ABC.
Vì H là trực tâm của tam giác ABC nên theo kết quả của Bài 4.15, phần a) trang 54 ta có →AH=2→IM (với M là trung điểm của BC).
Với A(1; 2), B(3; 4), C(2; –1) và I(154;54) ta có:
• Trung điểm M của BC có tọa độ là:
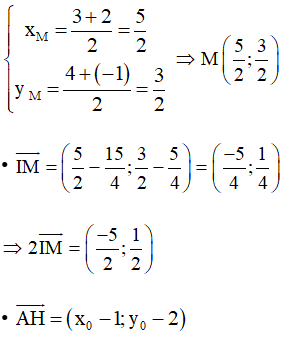
Ta có:
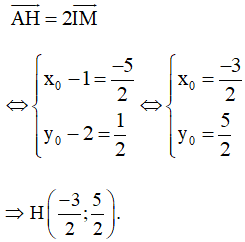
Vậy I(154;54) và H(−32;52).
Bài 4.28 trang 62 SBT Toán 10 Tập 1:
Lời giải:
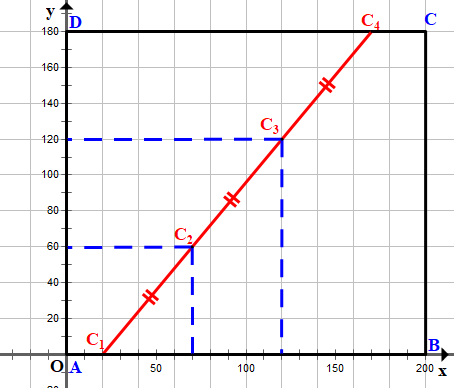
Chọn hệ trục tọa độ Oxy sao cho các đỉnh của hình hồ hình chữ nhật có các tọa độ là A(0; 0), B(200; 0), C(200; 180) và D(0; 180).
Gọi vị trí các cột điện được trồng là C1, C2, C3 và C4.
Vì vị trí cột điện thứ nhất C1 nằm trên bờ AB và cách A một khoảng 20 m nên trong hệ trục tọa độ đã chọn, điểm C1(20; 0).
Vị trí cột điện thứ tư nằm trên bờ CD và cách C một khoảng 30 m nên khoảng cách từ C4 đến D là 170 m. Khi đó trong hệ trục tọa độ đã chọn, điểm C4(170; 180).
Vì bốn cột điện được trồng liên tiếp nhau và cách đều trên một đường thẳng nên:
C1C2 = C2C3 = C3C4
⇒ C1C2 = 13C1C4 và C1C3 = 23C1C4.
⇒→C1C2=13→C1C4 và →C1C3=23→C1C4
Giả sử C2(a; b) và C3(x; y).
Với C1(20; 0), C4(170; 180) ta có:
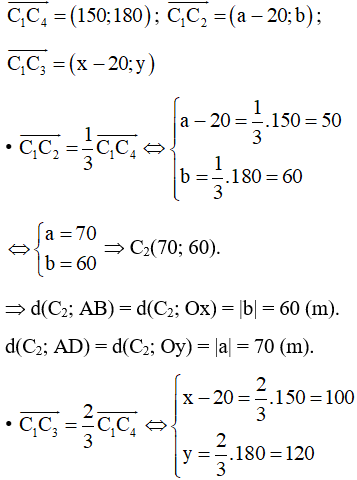
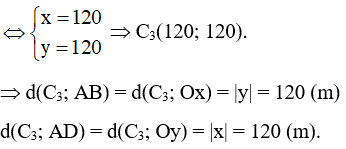
Vậy khoảng cách từ cột điện thứ hai đến bờ AB là 60 m và đến bờ AD là 70 m.
Khoảng cách từ cột điện thứ ba đến bờ AB là 120 m và đến bờ AD là 120 m.
Xem thêm lời giải sách bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:
Bài 8: Tổng và hiệu của hai vectơ
Bài 9: Tích của một vectơ với một số




