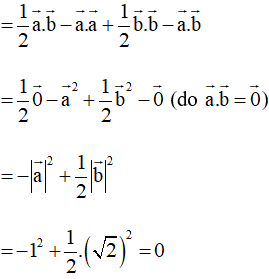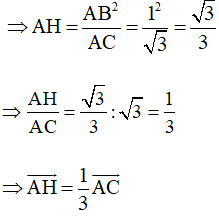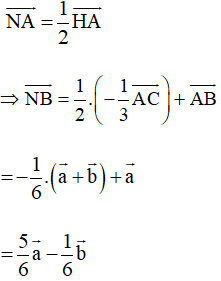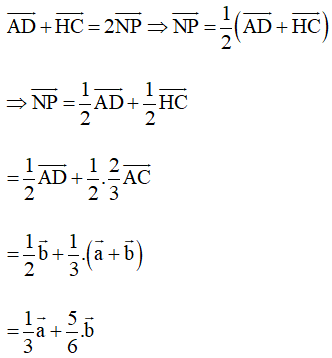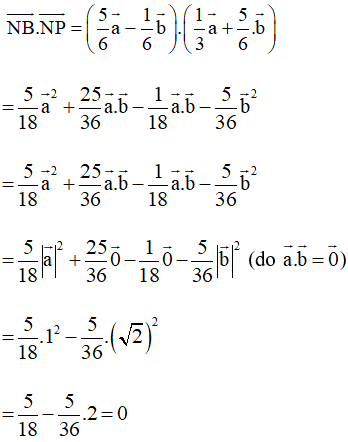Cho hình chữ nhật ABCD có AB = 1, BC = căn 2 Gọi M là trung điểm của AD. a) Chứng minh rằng
165
11/01/2024
Bài 4.30 trang 65 SBT Toán 10 Tập 1:
Cho hình chữ nhật ABCD có AB = 1, BC=√2. Gọi M là trung điểm của AD.
a) Chứng minh rằng các đường thẳng AC và BM vuông góc với nhau.
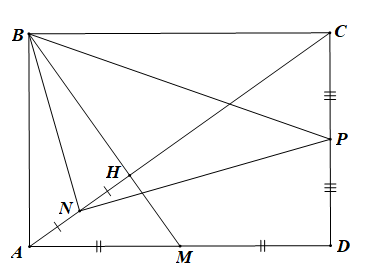
b) Gọi H là giao điểm của AC, BM. Gọi N là trung điểm của AH và P là trung điểm của CD. Chứng minh rằng tam giác NBP là một tam giác vuông.
Trả lời
a) Đặt →AB=→a,→AD=→b khi đó |→a|=1 và |→b|=√2.
Vì AB ⊥ AD nên →a⊥→b⇔→a.→b=→0
ABCD là hình chữ nhật nên cũng là hình bình hành nên ta có:
→AC=→AB+→AD=→a+→b (quy tắc hình bình hành)
M là trung điểm của AD nên →AM=12→AD=12→b
Suy ra →BM=→AM−→AB=12→b−→a
Khi đó →AC.→BM=(→a+→b).(12→b−→a)
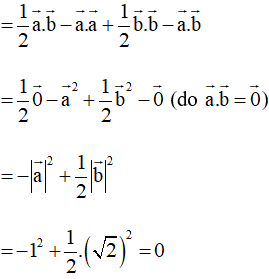
Do đó →AC.→BM=0⇔→AC⊥→BM
Þ AC ⊥ BM.
b) • Xét tam giác ABC vuông tại C, theo định lí Pythagore ta có:
AC2 = AB2 + BC2 = 1 + (√2)2= 3
⇒AC=√3
Theo hệ thức lượng trong tam giác vuông ta có:
AB2 = AH.AC
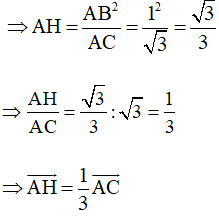
Khi đó →HC=23→AC và →HA=−13→AC
Ta có →NB=→NA+→AB (quy tắc ba điiểm)
Vì N là trung điểm của AH nên
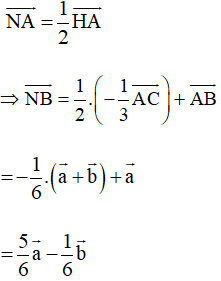
• Có N là trung điểm của HA và P là trung điểm của CD, theo kết quả bài 4.12, trang 58, Sách giáo khoa Toán 10, tập một, ta có:
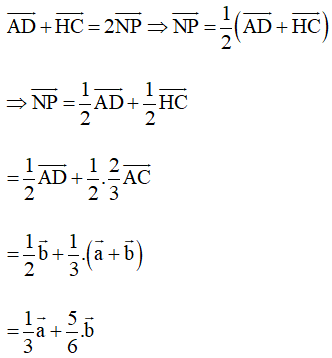
Khi đó
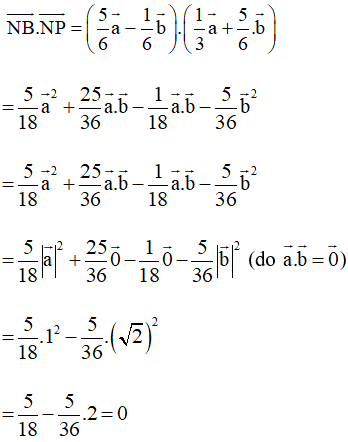
Do đó →NB.→NP=0⇒→NB⊥→NP
⇒ NB ⊥ NP.
Xem thêm các bài giải SBT Toán lớp 10 Kết nối tri thức hay, chi tiết khác:
Bài 9: Tích của một vectơ với một số
Bài 10: Vectơ trong mặt phẳng tọa độ
Bài 11: Tích vô hướng của hai vectơ
Bài tập cuối chương 4
Bài 12: Số gần đúng và sai số
Bài 13: Các số đặc trưng đo xu thế trung tâm