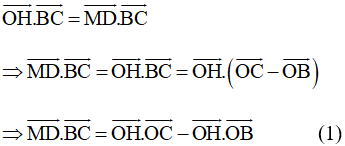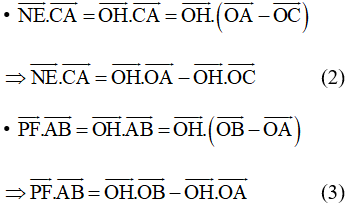Cho tam giác ABC không cân. Gọi D, E, F theo thứ tự là chân các đường cao kẻ từ A, B, C; gọi M, N, P

Bài 4.33 trang 65 SBT Toán 10 Tập 1:

Cho tam giác ABC không cân. Gọi D, E, F theo thứ tự là chân các đường cao kẻ từ A, B, C; gọi M, N, P tương ứng là trung điềm các cạnh BC, CA, AB. Chứng minh rằng:

$\overrightarrow{MD}.\overrightarrow{BC}+\overrightarrow{NE}.\overrightarrow{CA}+\overrightarrow{PF}.\overrightarrow{AB}=0$

Trả lời

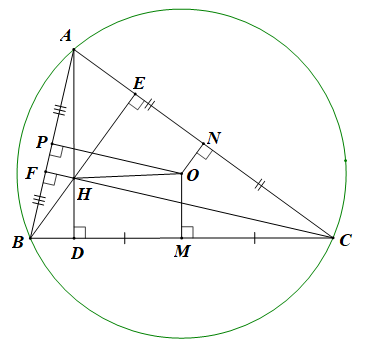
Gọi H và O là tâm đường tròn ngoại tiếp tam giác ABC.

• Vì D, M lần lượt là hình chiếu của H và O lên BC, nên $\overrightarrow{MD}$ là hình chiếu của $\overrightarrow{OH}$ trên giá của $\overrightarrow{BC}$

Theo định lí hình chiếu (được giới thiệu ở phần Nhận xét của Ví dụ 2, trang 62, Sách Bài tập Toán 10, tập một) ta có:

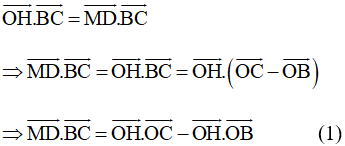
Chứng minh tương tự ta cũng có:

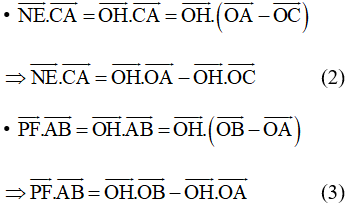
Từ (1), (2) và (3) ta có:

$\overrightarrow{MD}.\overrightarrow{BC}+\overrightarrow{NE}.\overrightarrow{CA}+\overrightarrow{PF}.\overrightarrow{AB}$

$=\overrightarrow{OH}.\overrightarrow{OC}-\overrightarrow{OH}.\overrightarrow{OB}+\overrightarrow{OH}.\overrightarrow{OA}$$-\overrightarrow{OH}.\overrightarrow{OC}+\overrightarrow{OH}.\overrightarrow{OB}-\overrightarrow{OH}.\overrightarrow{OA}$

= 0

Vậy $\overrightarrow{MD}.\overrightarrow{BC}+\overrightarrow{NE}.\overrightarrow{CA}+\overrightarrow{PF}.\overrightarrow{AB}=0.$

Xem thêm các bài giải SBT Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 9: Tích của một vectơ với một số

Bài 10: Vectơ trong mặt phẳng tọa độ

Bài 11: Tích vô hướng của hai vectơ

Bài tập cuối chương 4

Bài 12: Số gần đúng và sai số

Bài 13: Các số đặc trưng đo xu thế trung tâm