Bài 1 trang 78 SBT Toán 10 Tập 2: Trong mặt phẳng Oxy cho ba điểm A(2; 2); B(1; 3); C(– 1; 1).
a) Chứng minh OABC là một hình chữ nhật;
b) Tìm toạ độ tâm I của hình chữ nhật OABC.
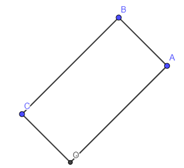
a) Ta có →OA=(2;2);→CB=(2;2),→OA=(−1;1) .
⇒→OA=→CB nên hai vectơ cùng phương hay OA song song với BC và OA = BC = √22+22=2√2 .
Do đó tứ giác OABC là hình bình hành.
Ta có →OA.→OC=2.(−1)+2.1=0 ⇒→OA⊥→OC hay OA ⊥ OC
Tứ giác OABC là hình bình hành và có 1 góc vuông nên tứ giác OABC là hình chữ nhật.
b) Tâm I(x; y) của hình chữ nhật OABC là trung điểm của OB
Ta có {x=xO+xB2=0+12=12y=yO+yB2=0+32=32
Vậy I(12;32).
Xem thêm các bài giải SBT Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Đường tròn trong mặt phẳng tọa độ
Bài 4: Ba đường conic trong mặt phẳng tọa độ