Trong không gian với hệ tọa độ Oxyz, từ điểm A (1;1;0) ta kẻ các tiếp tuyến đến mặt cầu (S) có tâm I (-1;1;1), bán kính R =1. Gọi M (a;b;c) là một trong các tiếp điểm ứng với các tiếp tuyến trên. Tìm giá trị lớn nhất của biểu thứcT=|2a−b+2c|
A. 3+√4115.
B. 3+√415.
C. 3+2√4115.
D. 3+2√415.
Đáp án đúng là: D
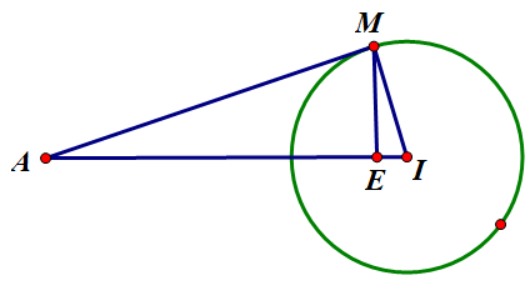
Do AM là tiếp tuyến của mặt cầu (S) nên AM⊥IM nên tam giác IAM vuông tại M
Xét ΔIAM , có: IA=√5, IM=1⇒MA=√IA2−R2=2
=> M thuộc mặt cầu tâm A bán kính là 2.
Khi đó M thuộc đường tròn giao tuyến (C) của mặt cầu tâm I bán kính R=1 và mặt cầu tâm A bán kính R=2.
(C)⊂(P):{(x+1)2+(y−1)2+(z−1)2=1(x−1)2+(y−1)2+z2=4
⇔(C)⊂(P):2x−z+2=0
Ta có IA:{x=1−2ty=1z=t,(t∈ℝ) .
Gọi E là tâm đường tròn giao tuyến.
Khi đó: E=IA∩(P)⇒E(−35;1;45) .
Xét ΔIAM có: r=EM=MA.MIIA=2√5 .
=> M thuộc mặt cầu tâm E(−35;1;45) bán kính R=2√5 hay (a+35)2+(b−1)2+(c−45)2=45 .
Do M∈(P)⇒2a−c+2=0⇔c=2a+2 .
Khi đó ta có được {(a+35)2+(b−1)2+(2a+65)2=45T=|6a−b+4|
(a+35)2+(b−1)2+(2a+65)2=45⇔(√5a+3√5)2+(b−1)2=45.
Ta có 6a−b+4=6√5(√5a+3√5)−(b−1)−35 .
Áp dụng bất đẳng thức Bunhiacopski, ta có:
|6√5(√5a+3√5)−(b−1)|≤√[(√5a+3√5)2+(b−1)2][(6√5)2+(−1)2]=2√415
.