Cho hàm số bậc ba y = f(x) có đồ thị là đường cong ở hình bên dưới.

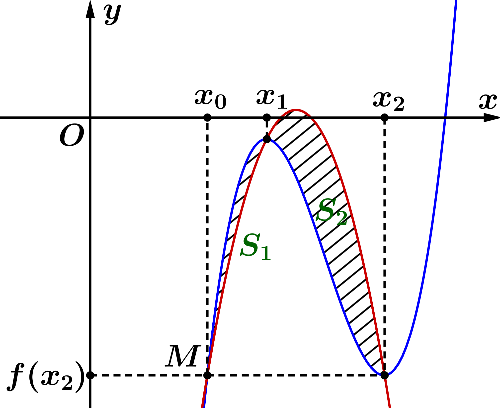
Gọi $x_1,x_2$  lần lượt là hai điểm cực trị thỏa mãn $x_2=x_1+2$  và $f\left(x_1\right)-3f\left(x_2\right)=0$.  và đồ thị luôn đi qua $M\left(x_0;f\left(x_0\right)\right)$, trong đó $x_0=x_1-1; g\left(x\right)$  là hàm số bậc hai có đồ thị qua 2 điểm cực trị của đồ thị hàm số y = f(x) và điểm M. Tính tỉ số $\frac{S_1}{S_2}$($S_1$ và $S_2$  lần lượt là diện tích hai hình phẳng được tạo bởi đồ thị hai hàm $f\left(x\right),g\left(x\right)$  như hình vẽ).

Đáp án đúng là: B

Khi ta tịnh tiến đồ thị sao cho $x_0=0$  khi đó diện tích hình phẳng không thay đổi.

$\Rightarrow x_1=1;x_2=3$ đặt $f\left(x\right)=a{x}^3+b{x}^2+cx+d;g\left(x\right)=m{x}^2+nx+q$

$\Rightarrow f^{\text{'}}\left(x\right)=3a{x}^2+2bx+c$

.

Vì hàm số y = f(x) đạt cực trị tại $x_1=1;x_2=3$và $f\left(1\right)-3f\left(3\right)=0$  nên ta có hệ phương trình:

$\left\{\begin{array}{l}3a+2b+c=0\\ 27a+6b+c=0\\ 80a+26b+8c+2d=0\end{array}\right.\iff \left\{\begin{array}{l}b=-6a\\ c=9a\\ d=2a\end{array}\right.$

$\Rightarrow f\left(x\right)=a\left(x^3-6x^2+9x+2\right)$

Mà hai đồ thị giao nhau tại 3 điểm nên ta có hệ phương trình:

$\left\{\begin{array}{l}g\left(0\right)=f\left(0\right)\\ g\left(1\right)=f\left(1\right)\\ g\left(2\right)=f\left(2\right)\end{array}\right.\iff \left\{\begin{array}{l}q=d=2a\\ m=-2a\\ n=6a\end{array}\right.\Rightarrow g\left(x\right)=a\left(-2x^2+6x+2\right)$

Khi đó $S_1=\left|a\right|.\underset{0}{\overset{1}{\int }}\left|x^3-4x^2+3x\right|\text{\hspace{0.17em}d}x=\frac{5\left|a\right|}{12};$

$S_2=\left|a\right|.\underset{1}{\overset{3}{\int }}\left|x^3-4x^2+3x\right|\text{\hspace{0.17em}d}x=\frac{8\left|a\right|}{3}$

.

Do đó $\frac{S_1}{S_2}=\frac{5}{32}$ .