Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ bên dưới. Số nghiệm thực của phương trình |f(x^4 - 2x^2)|=2
Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ bên dưới.
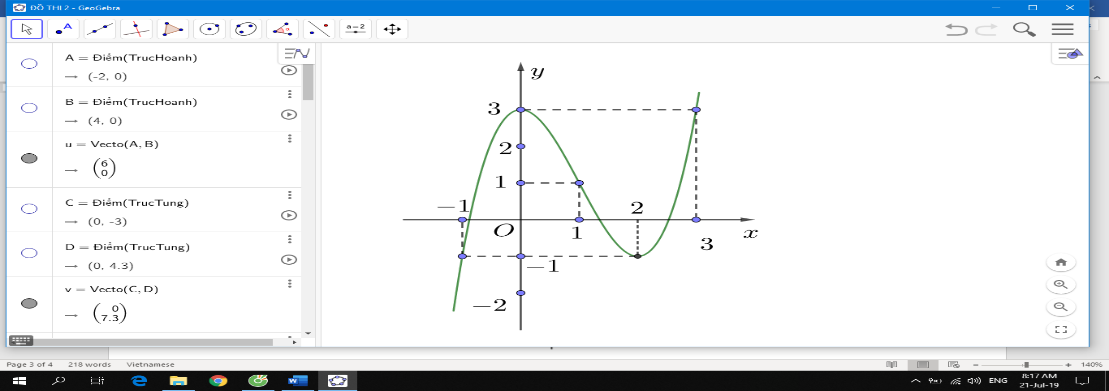
Số nghiệm thực của phương trình là
A. 7
B. 9
C. 10
D. 8
Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ bên dưới.

Số nghiệm thực của phương trình là
A. 7
B. 9
C. 10
D. 8
Đáp án đúng là: D
Phương trình
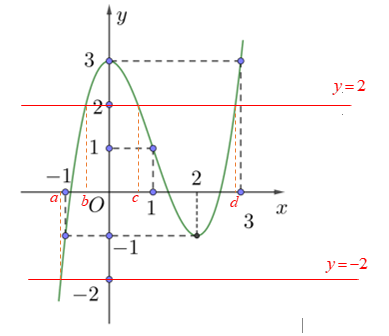
* Phương trình .
* Phương trình .
Bảng biến thiên của hàm số như sau:
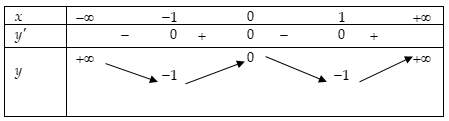
Dựa vào BBT trên ta có:
- Phương trình không có nghiệm thực.
- Phương trình có 4 nghiệm thực phân biệt.
- Phương trình có 2 nghiệm thực phân biệt.
- Phương trình có 2 nghiệm thực phân biệt.
Vậy phương trình có 8 nghiệm thực phân biệt.