Trong không gian Oxyz, cho hai điểm A (2;1;3), B (6;5;5). Xét khối nón (N) ngoại tiếp mặt cầu đường kính AB có B là tâm đường tròn đáy khối nón. Gọi S là đỉnh của khối nón (N). Khi thể tích khối nón (N) nhỏ nhất thì mặt phẳng qua đỉnh S và song song với mặt phẳng chứa đường tròn đáy của (N) có phương trình 2x + by + cz + d = 0. Tính T = b + c + d.

Đáp án đúng là: A

Mặt cầu (S) đường kính AB có tâm I (4;3;4), bán kính $R=\frac{AB}{2}=3$ .

Giả sử thiết diện qua trục hình nón là tam giác SMN.

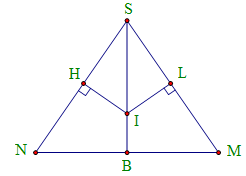
Gọi r, h  lần lượt là bán kính đáy và chiều cao của hình nón (h > 6).

I là tâm đường tròn nội tiếp của tam giác SMN ta có: $R=\frac{S_{SMN}}{P_{SMN}}$

$\Rightarrow 3=\frac{\frac{1}{2}MN.SB}{\frac{1}{2}\left(SM+SN+MN\right)}$ $\iff 3=\frac{r.h}{r+\sqrt{r^2+h^2}}$ $\iff 3\left(r+\sqrt{r^2+h^2}\right)=rh$ $\iff r^2=\frac{9h}{h-6}$.

Thể tích khối nón là $V=\frac{1}{3}\pi r^{2}h=\frac{\pi }{3}.\frac{9h^2}{h-6}=f\left(h\right)$ .

$f^{\text{'}}\left(h\right)=3\pi .\frac{h^2-12h}{{\left(h-6\right)}^2}$

.

$f^{\text{'}}\left(h\right)=0\iff \left[\begin{array}{l}h=0\\ h=12.\end{array}\right.$

Bảng biến thiên

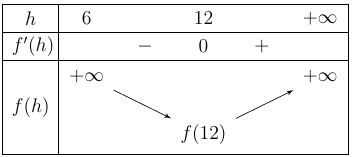
V đạt giá trị nhỏ nhất $\iff h=12$ .

Ta có $\overrightarrow{IS}=3\overrightarrow{BI}\Rightarrow S\left(-2;-3;1\right)$ .

Phương trình mặt phẳng (P) qua S (-2;-3;1), có vectơ pháp tuyến $\overrightarrow{AB}=2\left(2;2;1\right)$  là $2x+2y+z+9=0$ .

Suy ra b = 2; c = 1; d = 9.

Vậy T = b + c + d = 12.