Trong Hình 12, cho tứ giác ABCD là hình thang. Biết DB là tia phân giác của góc ADC và góc DAB = góc DBC

333 20/12/2023

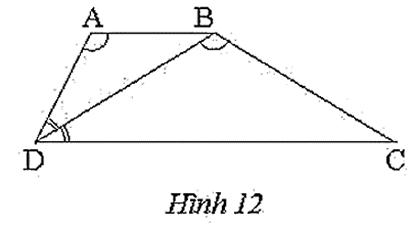
Bài 12 trang 64 SBT Toán 8 Tập 2: Trong Hình 12, cho tứ giác ABCD là hình thang. Biết DB là tia phân giác của $\hat{A D C}$ và $\hat{D A B} = \hat{D B C}$ . Chứng minh rằng:

a) ∆ABD ᔕ ∆BDC.

b) BD² = AB . DC.

Trong Hình 12, cho tứ giác ABCD là hình thang. Biết DB là tia phân giác của

Trả lời

a) Xét ∆ABD và ∆BDC có

$\hat{D A B} = \hat{D B C}$ và $\hat{A D B} = \hat{B D C}$ (DB là tia phân giác của $\hat{A D C}$ ).

Do đó ∆ABD ᔕ ∆BDC (g.g).

b) Ta có ∆ABD ᔕ ∆BDC, suy ra $\frac{A B}{B D} = \frac{B D}{D C}$ .

Do đó BD² = AB . DC (đpcm).

Xem thêm các bài giải sách bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 7

Bài 1: Hai tam giác đồng dạng

Bài 2: Các trường hợp đồng dạng của hai tam giác

Bài 3: Các trường hợp đồng dạng của hai tam giác vuông

Bài 4: Hai hình đồng dạng

Bài tập cuối chương 8

Các trường hợp đồng dạng của hai tam giác sbt

Câu hỏi cùng chủ đề

Cho tam giác ABC có ba góc nhọn. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho góc ADE = góc ACB

Bài 13 trang 65 SBT Toán 8 Tập 2. Cho tam giác ABC có ba góc nhọn. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho ADE^=ACB^. a) Chứng minh rằng ∆AED ᔕ ∆ABC. b) Tia phân giác của BAC^ cắt DE tại M và cắt BC tại N. Chứng minh rằng ME . NC = MD . NB.

Các trường hợp đồng dạng của hai tam giác sbt

887 1 năm trước

Quan sát Hình 11. Vẽ vào tờ giấy tam giác MNP với NP = 6 cm, góc N = 45 độ, góc P = 75 độ. Chứng minh rằng ∆MNP ᔕ ∆ABC

Bài 11 trang 64 SBT Toán 8 Tập 2. Quan sát Hình 11. Vẽ vào tờ giấy tam giác MNP với NP = 6 cm, N^=45°, P^=75°. a) Chứng minh rằng ∆MNP ᔕ ∆ABC. b) Dùng thước đo chiều dài cạnh MP của ∆MNP. Tính khoảng cách giữa hai điểm A và C ở hai bờ sông trong Hình 11.

Các trường hợp đồng dạng của hai tam giác sbt

203 1 năm trước

Trong Hình 10, cho biết AB = 4,2; IA = 6; IC = 10; góc ABI = 60°; góc CDx = 120°. Tính độ dài CD

Bài 10 trang 64 SBT Toán 8 Tập 2. Trong Hình 10, cho biết AB = 4,2; IA = 6; IC = 10; ABI^ = 60°; CDx^ = 120°. Tính độ dài CD.

Các trường hợp đồng dạng của hai tam giác sbt

173 1 năm trước

Quan sát Hình 9. Chứng minh rằng ∆ABC ᔕ ∆MNQ

Bài 9 trang 64 SBT Toán 8 Tập 2. Quan sát Hình 9. a) Chứng minh rằng ∆ABC ᔕ ∆MNQ. b) Tính x, y.

Các trường hợp đồng dạng của hai tam giác sbt

182 1 năm trước

Cho tam giác đều ABC, từ B và C kẻ các đường thẳng song song với AC và AB, hai đường này cắt nhau tại M

Bài 8 trang 64 SBT Toán 8 Tập 2. Cho tam giác đều ABC, từ B và C kẻ các đường thẳng song song với AC và AB, hai đường này cắt nhau tại M. Qua M kẻ đường thẳng cắt AB tại E và cắt AC tại F. Chứng minh rằng. a) CACF=MEMF và BEBA=MEMF. b) ∆BCE ᔕ ∆CFB.

Các trường hợp đồng dạng của hai tam giác sbt

194 1 năm trước

Cho tam giác ABC có AB = 12, AC = 15. Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh AC sao cho AM = 7,5 , AN = 6

Bài 7 trang 63 SBT Toán 8 Tập 2. Cho tam giác ABC có AB = 12, AC = 15. Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh AC sao cho AM = 7,5 , AN = 6. Chứng minh rằng. a) ∆ANM ᔕ ∆ABC. b) ABN^=ACM^.

Các trường hợp đồng dạng của hai tam giác sbt

221 1 năm trước

Quan sát Hình 8. Chứng minh rằng ∆ABC ᔕ ∆DEF

Bài 6 trang 63 SBT Toán 8 Tập 2. Quan sát Hình 8. a) Chứng minh rằng ∆ABC ᔕ ∆DEF. b) Cho biết AM là đường trung tuyến của tam giác ABC, DN là đường trung tuyến của tam giác DEF và AM = 5,1 cm. Tính độ dài DN.

Các trường hợp đồng dạng của hai tam giác sbt

201 1 năm trước

Quan sát Hình 7. Chứng minh rằng góc OBA = góc OAC

Bài 5 trang 63 SBT Toán 8 Tập 2. Quan sát Hình 7. Chứng minh rằng OBA^=OAC^.

Các trường hợp đồng dạng của hai tam giác sbt

253 1 năm trước

Anh Minh dự định thiết kế sân vườn nhà mình có hai bồn hoa hình tam giác đồng dạng với nhau (Hình 6). Bồn hoa thứ nhất có chu vi 7,5 m và cạnh dài nhất là 3,5 m

Bài 4 trang 63 SBT Toán 8 Tập 2. Anh Minh dự định thiết kế sân vườn nhà mình có hai bồn hoa hình tam giác đồng dạng với nhau (Hình 6). Bồn hoa thứ nhất có chu vi 7,5 m và cạnh dài nhất là 3,5 m. Bồn hoa thứ hai có chu vi 4,5 m. Tính độ dài cạnh dài nhất của bồn hoa thứ hai.

Các trường hợp đồng dạng của hai tam giác sbt

184 1 năm trước

Cho tam giác MAB và ABN như Hình 5. Biết MA = 10 cm, MB = 15 cm, AB = 8 cm, NA = 12 cm, NB = 6,4 cm. Chứng minh rằng: ∆MAB ᔕ ∆ABN

Bài 3 trang 63 SBT Toán 8 Tập 2. Cho tam giác MAB và ABN như Hình 5. Biết MA = 10 cm, MB = 15 cm, AB = 8 cm, NA = 12 cm, NB = 6,4 cm. Chứng minh rằng. a) ∆MAB ᔕ ∆ABN. b) Tứ giác AMBN là hình thang.

Các trường hợp đồng dạng của hai tam giác sbt

208 1 năm trước

Xem tất cả

Trong Hình 12, cho tứ giác ABCD là hình thang. Biết DB là tia phân giác của góc ADC và góc DAB = góc DBC

Trả lời

Câu hỏi cùng chủ đề

Cho tam giác ABC có ba góc nhọn. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho góc ADE = góc ACB

Quan sát Hình 11. Vẽ vào tờ giấy tam giác MNP với NP = 6 cm, góc N = 45 độ, góc P = 75 độ. Chứng minh rằng ∆MNP ᔕ ∆ABC

Trong Hình 10, cho biết AB = 4,2; IA = 6; IC = 10; góc ABI = 60°; góc CDx = 120°. Tính độ dài CD

Quan sát Hình 9. Chứng minh rằng ∆ABC ᔕ ∆MNQ

Cho tam giác đều ABC, từ B và C kẻ các đường thẳng song song với AC và AB, hai đường này cắt nhau tại M

Cho tam giác ABC có AB = 12, AC = 15. Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh AC sao cho AM = 7,5 , AN = 6

Quan sát Hình 8. Chứng minh rằng ∆ABC ᔕ ∆DEF

Quan sát Hình 7. Chứng minh rằng góc OBA = góc OAC

Anh Minh dự định thiết kế sân vườn nhà mình có hai bồn hoa hình tam giác đồng dạng với nhau (Hình 6). Bồn hoa thứ nhất có chu vi 7,5 m và cạnh dài nhất là 3,5 m

Cho tam giác MAB và ABN như Hình 5. Biết MA = 10 cm, MB = 15 cm, AB = 8 cm, NA = 12 cm, NB = 6,4 cm. Chứng minh rằng: ∆MAB ᔕ ∆ABN

Danh mục