Tìm các giá trị thực của tham số m sao cho điểm cực tiểu của đồ thị hàm số y=x^3+x^2+mx-1 nằm bên phải trục tung.
56
19/04/2024
Tìm các giá trị thực của tham số m sao cho điểm cực tiểu của đồ thị hàm số y=x3+x2+mx−1 nằm bên phải trục tung.
A. m<0
B. 0<m<13
C. m<13
D. Không tồn tại.
Trả lời
Hướng dẫn giải
Ta có: y' .
Đồ thị hàm số có điểm cực tiểu khi phương trình có hai nghiệm phân biệt
Khi đó, giả sử , (với ) là hai nghiệm của phương trình thì
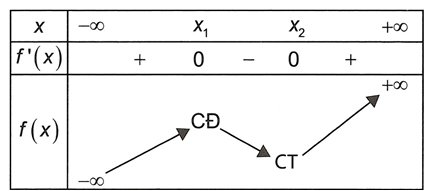
Bảng biến thiên
Do nên điểm cực tiểu của đồ thị hàm số nằm bên phải trục tung (2) .
Từ (1), (2) ta có
Chọn A.