Tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC. Chứng minh rằng góc BAC = 90 độ 

ài 75 trang 90 SBT Toán 7 Tập 2: Tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC. Chứng minh rằng góc BAC = 90 độ 

Trả lời

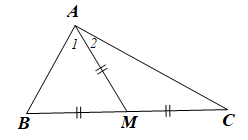
Ta có: AM = $\frac{1}{2}$BC, BM = MC nên AM = BM = MC.

Suy ra hai tam giác AMB và AMC cân tại M.

Do đó $\widehat{B}={\widehat{A}}_1,\widehat{C}={\widehat{A}}_2$

Xét $∆$ABC có $\widehat{B}+\widehat{C}+\widehat{BAC}=180°$ (tổng ba góc của một tam giác)

Suy ra ${\widehat{A}}_1+{\widehat{A}}_2+\widehat{BAC}=180°$ hay $\widehat{BAC}+\widehat{BAC}=180°$

Nên $2\widehat{BAC}=180°$

Do đó $\widehat{BAC}=\frac{180°}{2}=90°$

Vậy $\widehat{BAC}=90°$.

Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 8. Đường vuông góc và đường xiên

Bài 9. Đường trung trực của một đoạn thẳng

Bài 10. Tính chất ba đường trung tuyến của tam giác

Bài 11. Tính chất ba đường phân giác của tam giác

Bài 12. Tính chất ba đường trung trực của tam giác

Bài 13. Tính chất ba đường cao của tam giác