Cho tam giác ABC có trọng tâm G. Gọi M là trung điểm của BC. Trên tia đối của MG lấy điểm D sao cho MD = MG. a) Chứng minh CG là trung tuyến của tam

Bài 71 trang 89, 90 SBT Toán 7 Tập 2: Cho tam giác ABC có trọng tâm G. Gọi M là trung điểm của BC. Trên tia đối của MG lấy điểm D sao cho MD = MG.

a) Chứng minh CG là trung tuyến của tam giác ACD.

b) Chứng minh BG song song với CD.

c) Gọi I là trung điểm của BD; AI cắt BG tại F. Chứng minh AF = 2FI.

Trả lời

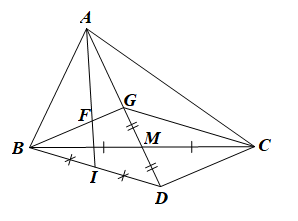
a) Vì G là trọng tâm tam giác ABC nên GM = $\frac{1}{2}$GA.

Mà MD = MG (giả thiết) nên M là trung điểm của GD và GM = $\frac{1}{2}$GD.

Suy ra GD = GA.

Do đó CG là trung tuyến của tam giác ACD.

Vậy CG là trung tuyến của tam giác ACD.

b) Xét $∆$BGM và $∆$CDM có:

GM = DM (giả thiết),

$\widehat{GMB}=\widehat{DMC}$ (hai góc đối đỉnh),

MB = MC (vì M là trung điểm của BC)

Nên ∆BGM = ∆CDM (c.g.c).

Suy ra $\widehat{BGM}=\widehat{CDM}$ (hai góc tương ứng).

Mà chúng ở vị trí so le trong nên BG // CD.

Vậy BG // CD.

c) Trong tam giác ABD có AI và BG là hai đường trung tuyến, AI và BG cắt nhau tại F.

Do đó F là trọng tâm của tam giác ABD.

Suy ra FI = $\frac{1}{2}$FA hay AF = 2FI.

Vậy AF = 2FI.

Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 8. Đường vuông góc và đường xiên

Bài 9. Đường trung trực của một đoạn thẳng

Bài 10. Tính chất ba đường trung tuyến của tam giác

Bài 11. Tính chất ba đường phân giác của tam giác

Bài 12. Tính chất ba đường trung trực của tam giác

Bài 13. Tính chất ba đường cao của tam giác