Cho G là trọng tâm của tam giác ABC và điểm M tùy ý. Chứng minh rằng vectơ MA + vectơ MB + vectơ MC = 3(vectơ MG)

Hoạt động 4 trang 90 Toán lớp 10 Tập 1: Cho G là trọng tâm của tam giác ABC và điểm M tùy ý. Chứng minh rằng $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$

Trả lời

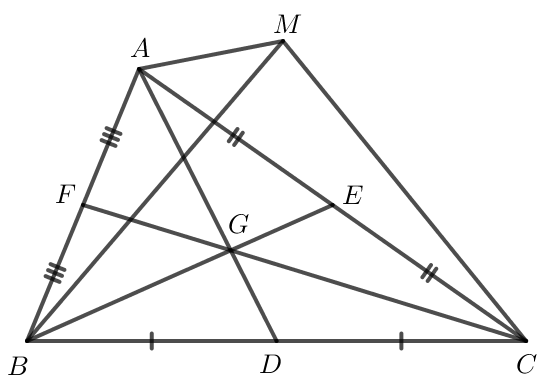
Gọi D, E, F lần lượt là trung điểm của BC, AC, AB.

Do D là trung điểm của BC nên $\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{A\text{D}}$.

Do E là trung điểm của AC nên $\overrightarrow{BA}+\overrightarrow{BC}=2\overrightarrow{BE}$.

Do F là trung điểm của AB nên $\overrightarrow{CA}+\overrightarrow{CB}=2\overrightarrow{CF}$.

Do đó $\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{CA}+\overrightarrow{CB}=2\overrightarrow{A\text{D}}+2\overrightarrow{BE}+2\overrightarrow{CF}$.

$\Rightarrow \overrightarrow{AB}+\overrightarrow{BA}+\overrightarrow{AC}+\overrightarrow{CA}+\overrightarrow{BC}+\overrightarrow{CB}=2\overrightarrow{A\text{D}}+2\overrightarrow{BE}+2\overrightarrow{CF}$.

$\Rightarrow 2\overrightarrow{A\text{D}}+2\overrightarrow{BE}+2\overrightarrow{CF}=\overrightarrow{0}$

$\Rightarrow \overrightarrow{A\text{D}}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{0}$

$\Rightarrow -\left(\overrightarrow{A\text{D}}+\overrightarrow{BE}+\overrightarrow{CF}\right)=\overrightarrow{0}$

$\Rightarrow -\overrightarrow{A\text{D}}-\overrightarrow{BE}-\overrightarrow{CF}=\overrightarrow{0}$

$\Rightarrow \overrightarrow{\text{DA}}+\overrightarrow{EB}+\overrightarrow{FC}=\overrightarrow{0}$

Do G là trọng tâm của tam giác ABC nên

$\overrightarrow{GA}=\frac{2}{3}\overrightarrow{DA}$; $\overrightarrow{GB}=\frac{2}{3}\overrightarrow{EB}$; $\overrightarrow{GC}=\frac{2}{3}\overrightarrow{FC}$.

Do đó $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\frac{2}{3}\left(\overrightarrow{\text{DA}}+\overrightarrow{EB}+\overrightarrow{FC}\right)=\overrightarrow{0}$.

Ta có $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}$

$=3\overrightarrow{MG}+\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)$

$=3\overrightarrow{MG}$

Vậy $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$.

Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh Diều hay, chi tiết khác:

Bài 3: Khái niệm vectơ

Bài 4: Tổng và hiệu của hai vectơ

Bài 5: Tích của một số với một vectơ

Bài 6: Tích vô hướng của hai vectơ

Bài tập cuối chương 4

Chủ đề 1: Đo góc