Cho tứ giác ABCD có M, N lần lượt là trung điểm của hai cạnh AB và CD. Gọi G là trung điểm của đoạn thẳng MN, E là trọng tâm của tam giác BCD. Chứng minh

Bài 5 trang 92 Toán lớp 10 Tập 1: Cho tứ giác ABCD có M, N lần lượt là trung điểm của hai cạnh AB và CD. Gọi G là trung điểm của đoạn thẳng MN, E là trọng tâm của tam giác BCD. Chứng minh:

a) $\overrightarrow{EA}+\overrightarrow{EB}+\overrightarrow{EC}+\overrightarrow{ED}=4\overrightarrow{EG}$;

b) $\overrightarrow{EA}=4\overrightarrow{EG}$;

c) Điểm G thuộc đoạn thẳng AE và $\overrightarrow{AG}=\frac{3}{4}\overrightarrow{AE}$.

Trả lời

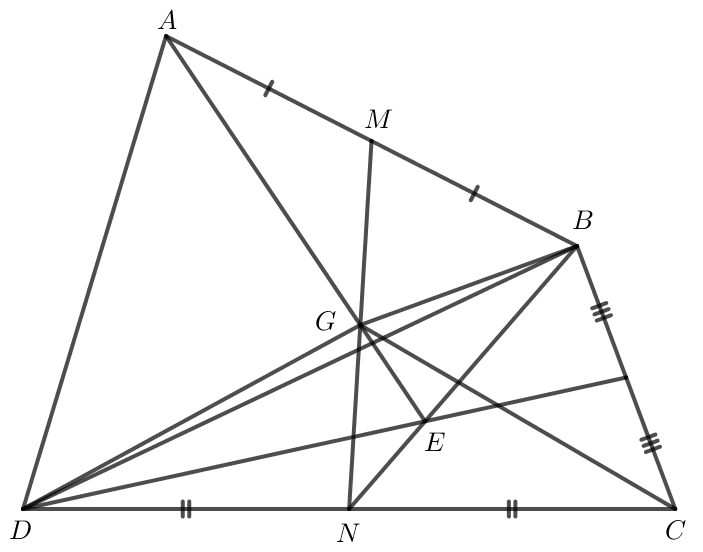
a) Do M là trung điểm của AB nên $\overrightarrow{GA}+\overrightarrow{GB}=2\overrightarrow{GM}$ (1).

Do N là trung điểm của CD nên $\overrightarrow{GC}+\overrightarrow{G\text{D}}=2\overrightarrow{GN}$ (2).

Do G là trung điểm của MN nên GM = GN.

Ta thấy hai vectơ $\overrightarrow{GM}$ và $\overrightarrow{GN}$ ngược hướng và GM = GN nên $\overrightarrow{GM}=-\overrightarrow{GN}$.

Do đó $\overrightarrow{GM}+\overrightarrow{GN}=-\overrightarrow{GN}+\overrightarrow{GN}=\overrightarrow{0}$.

Từ (1) và (2) ta có $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{G\text{D}}=2\overrightarrow{GM}+2\overrightarrow{GN}=2\left(\overrightarrow{GM}+\overrightarrow{GN}\right)=\overrightarrow{0}$.

Ta có

$$\begin{gathered} \overrightarrow{E\text{A}}+\overrightarrow{EB}+\overrightarrow{EC}+\overrightarrow{E\text{D}} \\ =\overrightarrow{EG}+\overrightarrow{\text{GA}}+\overrightarrow{EG}+\overrightarrow{\text{GB}}+\overrightarrow{EG}+\overrightarrow{\text{GC}}+\overrightarrow{EG}+\overrightarrow{\text{GD}} \end{gathered}$$.

$=4\overrightarrow{EG}+\left(\overrightarrow{\text{GA}}+\overrightarrow{\text{GB}}+\overrightarrow{\text{GC}}+\overrightarrow{\text{GD}}\right)$

$=4\overrightarrow{EG}$

Vậy $\overrightarrow{EA}+\overrightarrow{EB}+\overrightarrow{EC}+\overrightarrow{ED}=4\overrightarrow{EG}$.

b) Do E là trọng tâm của tam giác BCD nên $\overrightarrow{EB}+\overrightarrow{EC}+\overrightarrow{ED}=\overrightarrow{0}$.

Do đó $\overrightarrow{EA}=4\overrightarrow{EG}$.

c) Do $\overrightarrow{EA}=4\overrightarrow{EG}$ nên hai vectơ $\overrightarrow{E\text{A}}$ và $\overrightarrow{EG}$ cùng hướng.

Mà 4 > 0 nên G nằm giữa A và E.

Do đó $\left|\overrightarrow{EA}\right|=4\left|\overrightarrow{EG}\right|$ hay EA = 4EG.

$\Rightarrow$ EG = $\frac{1}{4}$EA

$\Rightarrow$ AG = $\frac{3}{4}$EA.

Ta thấy hai vectơ $\overrightarrow{AG}$ và $\overrightarrow{A\text{E}}$ cùng hướng và AG = $\frac{3}{4}$EA nên $\overrightarrow{AG}=\frac{3}{4}\overrightarrow{A\text{E}}$.

Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh Diều hay, chi tiết khác:

Bài 3: Khái niệm vectơ

Bài 4: Tổng và hiệu của hai vectơ

Bài 5: Tích của một số với một vectơ

Bài 6: Tích vô hướng của hai vectơ

Bài tập cuối chương 4

Chủ đề 1: Đo góc