Cho (un) là cấp số cộng có u2 + u4 = 22, u1 . u5 = 21 và công sai d dương. a) Tính

Bài 24 trang 50 SBT Toán 11 Tập 1: Cho (u_n) là cấp số cộng có u₂ + u₄ = 22, u₁ . u₅ = 21 và công sai d dương.

a) Tính u₁₀₀, S₁₀₀.

b) Tính tổng: u₁ + u₅ + u₉ + ... + u₁₀₁.  

Trả lời

Ta có u₂ + u₄ = (u₁ + d) + (u₁ + 3d) = 2u₁ + 4d = 22, suy ra 4d = 22 – 2u₁.

Lại có u₁ . u₅ = u₁ . (u₁ + 4d) = u₁ . (u₁ + 22 – 2u₁) = u₁ . (22 – u₁).

Mà u₁ . u₅ = 21, do đó u₁ . (22 – u₁) = 21 ⇔ 22u₁ – u₁² – 21 = 0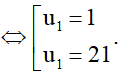 

Với u₁ = 1, suy ra $d=\frac{22-2u_1}{4}=\frac{22-2.1}{4}=5>0$  (thỏa mãn).

Với u₁ = 21, suy ra $d=\frac{22-2u_1}{4}=\frac{22-2.21}{4}=-5<0$  (không thỏa mãn).

Vậy cấp số cộng (u_n) có số hạng đầu u₁ = 1 và công sai d = 5.

a) Ta có: u₁₀₀ = u₁ + (100 – 1)d = 1 + 99 . 5 = 496.

.

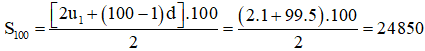b) Ta có u₅ – u₁ = (u₁ + 4d) – u₁ = 4d, tương tự u₉ – u₅ = 4d, ...

Do đó các số u₁, u₅, u₉, ..., u₁₀₀ lập thành một cấp số cộng có số hạng đầu u₁ = 1 và công sai d' = 4d = 4 . 5 = 20.

Lại có (101 – 1) : 4 + 1 = 26 nên tổng u₁ + u₅ + u₉ + ... + u₁₀₁ gồm 26 số hạng.

Do vậy, u₁ + u₅ + u₉ + ... + u₁₀₁  .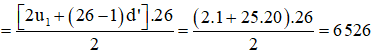

Xem thêm lời giải bài tập SBT Toán 11 Cánh diều hay, chi tiết khác:

Bài tập cuối chương 1

Bài 1: Dãy số

Bài 2: Cấp số cộng

Bài 3: Cấp số nhân

Bài tập cuối chương 2

Bài 1: Giới hạn của dãy số
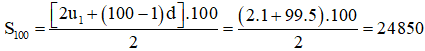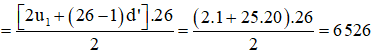