Cho tứ giác ABCD với AB = 2 cm, AD = 3 cm, BD = 4 cm, BC = 6 cm, CD = 8 cm. Chứng minh rằng ∆ABD ᔕ ∆BDC và AB song song với CD.

Trả lời

Lời giải

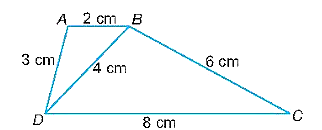
Tam giác ABD và tam giác BDC có:

\(\frac{{AB}}{{BD}} = \frac{{BD}}{{DC}} = \frac{{AD}}{{BC}}\)           (do \(\frac{2}{4} = \frac{4}{8} = \frac{3}{6} = \frac{1}{2}\))

Do đó, ∆ABD ᔕ ∆BDC (c.c.c).

Suy ra: \(\widehat {ABD} = \widehat {BDC}\) (hai góc tương ứng).

Mà hai góc này ở vị trí so le trong. Do đó, AB song song với CD.