Cho hai điểm M, N lần lượt nằm trên hai cạnh AB, AC của tam giác ABC sao cho AM . AB = AN . AC.
a) Chứng minh rằng ∆AMN ᔕ ∆ACB.
b) Lấy E, F lần lượt là trung điểm của MN, BC. Chứng minh rằng \(\widehat {EAB} = \widehat {FAC}\).
Lời giải
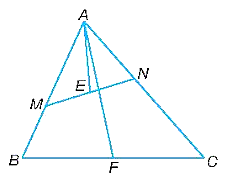
a)
Vì AM . AB = AN . AC nên \(\frac{{AM}}{{AC}} = \frac{{AN}}{{AB}}\).
Tam giác AMN và tam giác ABC có:
\(\frac{{AM}}{{AC}} = \frac{{AN}}{{AB}}\),
\(\widehat {BAC}\) chung.
Do đó, ∆AMN ᔕ ∆ACB (c.g.c).
b)
Vì ∆AMN ᔕ ∆ACB (cmt) nên \(\widehat {AMN} = \widehat C\) và \(\frac{{AM}}{{AC}} = \frac{{MN}}{{CB}}\).
Mà E, F lần lượt là trung điểm của MN, BC nên MN = 2ME, BC = 2FC.
Do đó: \(\frac{{AM}}{{AC}} = \frac{{MN}}{{CB}} = \frac{{2ME}}{{2FC}} = \frac{{ME}}{{FC}}\).
Tam giác MAE và tam giác CAF có:
\(\widehat {AME} = \widehat C\) (do \(\widehat {AMN} = \widehat C\));
\(\frac{{AM}}{{AC}} = \frac{{ME}}{{FC}}\) (cmt).
Do đó, ∆AME ᔕ ∆ACF (c.g.c). Suy ra \(\widehat {EAM} = \widehat {FAC}\) (hai góc tương ứng).
Vậy \(\widehat {EAB} = \widehat {FAC}\).