Cho tam giác ABC với AB = 6 cm, AC = 4 cm, BC = 5 cm. Trên tia đối của tia CA lấy điểm D sao cho CD = CB. Chứng minh rằng:
a) ∆ABC ᔕ ∆ADB.
b) \(\widehat {ACB} = 2\widehat {ABC}\).
Lời giải
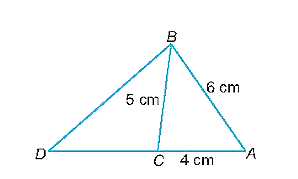
a)
Ta có: AD = AC + DC = AC + BC = 4 + 5 = 9 (cm).
Xét tam giác ABC và tam giác ADB có:
\(\widehat A\) chung
\(\frac{{AB}}{{AD}} = \frac{{AC}}{{AB}}\,\,\left( {\frac{6}{9} = \frac{4}{6}} \right)\).
Do đó, ∆ABC ᔕ ∆ADB (c.g.c).
b)
Vì ∆ABC ᔕ ∆ADB (cmt) nên \(\widehat {ABC} = \widehat {ADB}\).
Mà tam giác BCD cân tại C (do CD = CB) nên \(\widehat {CBD} = \widehat {BDC}\) hay \(\widehat {CBD} = \widehat {ADB}\).
Do đó, \(\widehat {CBD} = \widehat {ABC}\).
Vì góc ACB là góc ngoài tại đỉnh C của tam giác DBC nên ta có:
\(\widehat {ACB} = \widehat {CDB} + \widehat {CBD} = 2\widehat {CBD} = 2\widehat {ABC}\).
Vậy \(\widehat {ACB} = 2\widehat {ABC}\).