Cho tam giác ABC và hai điểm P, Q lần lượt nằm trên các tia đối của tia AB và AC sao cho \(\widehat {APQ} = \widehat {ACB}\). Chứng minh rằng:

a) AP . AB = AQ . AC.

b) ∆APC ᔕ ∆AQB.

Lời giải

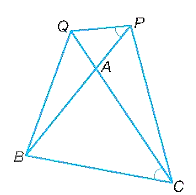
a)

Xét tam giác APQ và tam giác ACB có:

\(\widehat {PAQ} = \widehat {BAC}\) (hai góc đối đỉnh)

\(\widehat {APQ} = \widehat {ACB}\) (giả thiết)

Do đó, ∆APQ ᔕ ∆ACB (g.g) nên \(\frac{{AP}}{{AC}} = \frac{{AQ}}{{AB}}\).

Suy ra: AP . AB = AQ . AC.

b)

Vì \(\frac{{AP}}{{AC}} = \frac{{AQ}}{{AB}}\) nên \(\frac{{AP}}{{AQ}} = \frac{{AC}}{{AB}}\).

Xét tam giác APC và tam giác AQB có:

\(\widehat {PAC} = \widehat {BAQ}\) (hai góc đối đỉnh),

\(\frac{{AP}}{{AQ}} = \frac{{AC}}{{AB}}\) (chứng minh trên).

Do đó, ∆APC ᔕ ∆AQB (c.g.c).