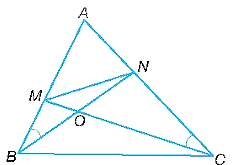
Cho hai điểm M, N lần lượt nằm trên các cạnh AB, AC của tam giác ABC sao cho \(\widehat {ABN} = \widehat {ACM}\). Gọi O là giao điểm của BN và CM. Chứng minh rằng:

a) AM . AB = AN . AC.

b) OM . OC = ON . OB.

Lời giải

a)

Xét tam giác ABN và tam giác ACM có:

\(\widehat A\) chung

\(\widehat {ABN} = \widehat {ACM}\) (gt)

Do đó, ∆ABN ᔕ ∆ACM (g.g).

Suy ra \(\frac{{AB}}{{AC}} = \frac{{AN}}{{AM}}\) nên AM . AB = AN . AC.

b)

Tam giác BOM và tam giác CON có:

\(\widehat {MBO} = \widehat {NCO}\) (do \(\widehat {ABN} = \widehat {ACM}\))

\(\widehat {MOB} = \widehat {NOC}\) (hai góc đối đỉnh)

Nên ∆BOM ᔕ ∆CON (g.g).

Suy ra \(\frac{{OM}}{{ON}} = \frac{{OB}}{{OC}}\) nên OM . OC = ON . OB.