Cho tam giác ABC và hai điểm M, N lần lượt nằm trên hai cạnh AB, AC sao cho MN song song với BC. Gọi ME, BF lần lượt là phân giác của các góc M, B của các tam giác AMN và tam giác ABC. Chứng minh rằng:

a) ∆MEN ᔕ ∆BFC.

b) $\frac{{AE}}{{AF}} = \frac{{MN}}{{BC}}$.

Lời giải

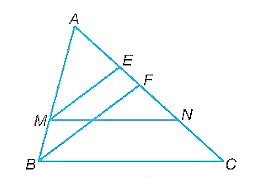
a)

Vì MN song song với BC (gt) nên

$\widehat {ENM} = \widehat C$ (hai góc đồng vị);

$\widehat {AMN} = \widehat {ABC}$ (hai góc đồng vị).

Mà ME, BF lần lượt là phân giác của các góc M, B của các tam giác AMN và tam giác ABC nên $\widehat {EMN} = \frac{1}{2}\widehat {AMN}$ và $\widehat {FBC} = \frac{1}{2}\widehat {ABC}$. Do đó, $\widehat {EMN} = \widehat {FBC}$.

Tam giác MEN và tam giác BFC có:

$\widehat {ENM} = \widehat C$ (cmt)

$\widehat {EMN} = \widehat {FBC}$ (cmt)

Do đó, tam giác MEN đồng dạng với tam giác BFC (g.g).

b)

Tam giác ABC có:

MN song song với BC

Nên theo hệ quả định lý Thalès ta có:

$\frac{{MN}}{{BC}} = \frac{{AM}}{{AB}}$ (1).

Vì ME, BF lần lượt là phân giác của $\widehat M$, $\widehat B$ của tam giác AMN và tam giác ABC nên $\widehat {EMA} = \frac{1}{2}\widehat {AMN} = \frac{1}{2}\widehat {ABC} = \widehat {FBA}$.

Do đó, $\widehat {EMA} = \widehat {FBA}$ mà hai góc này ở vị trí đồng vị nên ME song song với BF.

Tam giác ABF có ME song song với BF nên theo hệ quả định lý Thalès ta có:

$\frac{{AE}}{{AF}} = \frac{{AM}}{{AB}}$ (2).

Từ (1) và (2) ta có: $\frac{{AE}}{{AF}} = \frac{{MN}}{{BC}}$.