Cho tứ giác ABCD. Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi vectơ AB = vectơ DC
Bài 4 trang 86 Toán lớp 10 Tập 1: Cho tứ giác ABCD. Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi →AB=→DC.
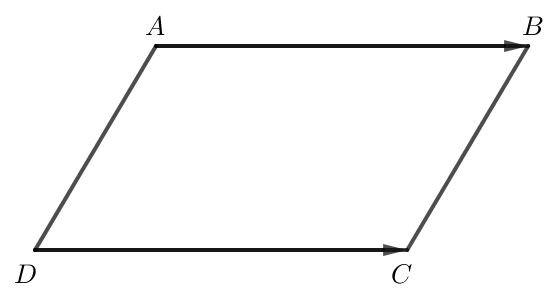
Phần thuận: ABCD là hình bình hành thì →AB=→DC.
Do ABCD là hình hình bình hành nên AB = DC và AB // DC.
Khi đó ta thấy hai vectơ →AB và vectơ →DC cùng hướng.
Mà AB = DC nên →AB=→DC.
Phần đảo: Tứ giác ABCD có →AB=→DC thì ABCD là hình bình hành.
Giá của vectơ →AB là đường thẳng AB, giá của vectơ →DC là đường thẳng DC.
Do →AB=→DC nên đường thẳng AB và đường thẳng DC song song hoặc trùng nhau.
Do A, B, C, D là 4 đỉnh của tứ giác nên hai đường thẳng AB và DC không trùng nhau.
Do đó đường thẳng AB và đường thẳng DC song song với nhau.
Mà →AB=→DC nên |→AB|=|→DC| hay AB = CD.
Tứ giác ABCD có AB // CD và AB = CD nên tứ giác ABCD là hình bình hành.
Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Giải tam giác và ứng dụng thực tế
Bài 2: Tổng và hiệu của hai vectơ