Cho tam giác nhọn ABC, các đường cao AD, BE, CF cắt nhau tại H. Chứng mình rằng: AD . BH = AC . BD

Bài 7 trang 75 SBT Toán 8 Tập 2: Cho tam giác nhọn ABC, các đường cao AD, BE, CF cắt nhau tại H. Chứng mình rằng:

a) AD . BH = AC . BD.

b) HA . HD = HB . HE = HC . HF.

c) BC² = BE . BH + CF . CH.

Trả lời

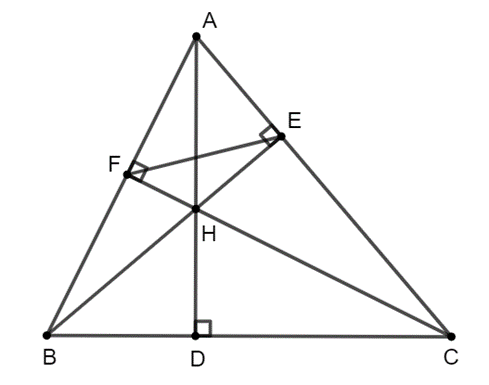
a) Ta có $\widehat{AHE}=\widehat{ACD}$ (cùng phụ với $\widehat{CAD}$).

Mà $\widehat{AHE}=\widehat{BHD}$ (đối đỉnh) nên $\widehat{ACD}=\widehat{BHD}$.

Xét ∆ADC vuông tại D và ∆BDH vuông tại D có $\widehat{ACD}=\widehat{BHD}$.

Do đó ∆ADC ᔕ ∆BDH (g.g).

Suy ra $\frac{AD}{BD}=\frac{AC}{BH}$. Do đó AD . BH = AC . BD (đpcm).

b) Xét ∆HEA vuông tại E và ∆HDB vuông tại D có $\widehat{AHE}=\widehat{BHD}$ (đối đỉnh).

Do đó ∆HEA ᔕ ∆HDB (g.g).

Suy ra $\frac{HE}{HD}=\frac{HA}{HB}$. Do đó HA . HD = HB . HE (1)

Xét ∆HFA vuông tại F và ∆HDC vuông tại D có $\widehat{AHF}=\widehat{CHD}$ (đối đỉnh).

Do đó ∆HFA ᔕ ∆HDC (g.g).

Suy ra $\frac{HF}{HD}=\frac{HA}{HC}$. Do đó HA . HD = HC . HF (2)

Từ (1) và (2) suy ra HA . HD = HB . HE = HC . HF (đpcm).

c) Xét ∆BEC vuông tại E và ∆BHD vuông tại D có $\widehat{EBC}$ chung.

Do đó ∆BEC ᔕ ∆BHD (g.g).

Suy ra $\frac{BC}{BH}=\frac{BE}{BD}$. Do đó BC . BD = BE . BH (3)

Xét ∆BCF vuông tại F và ∆HCD vuông tại D có $\widehat{FCB}$ chung.

Do đó ∆BCF ᔕ ∆HCD (g.g)

Suy ra $\frac{BC}{HC}=\frac{CF}{DC}$. Do đó BC . DC = CF . HC. (4)

Từ (3) và (4), suy ra BC . DB + BC . DC = BE . BH + CF . HC.

Do đó BC² = BE . BH + CF . CH (đpcm).

Xem thêm các bài giải sách bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 3: Các trường hợp đồng dạng của hai tam giác vuông

Bài 4: Hai hình đồng dạng

Bài tập cuối chương 8

Bài 1: Mô tả xác suất bằng tỉ số

Bài 2: Xác suất lí thuyết và xác suất thực nghiệm

Bài tập cuối chương 9