Bài 6 trang 75 SBT Toán 8 Tập 2: Cho tam giác ABC vuông tại A (AB < AC), M là điểm bất kì trên cạnh AC. Kẻ MD ⊥ BC (D ∈ BC).
a) Chứng minh rằng ∆DMC ᔕ ∆ABC.
b) Gọi E là giao điểm của đường thẳng AB với đường thẳng MD.
Chứng minh rằng DB . DC = DE . DM.
c) Đường thẳng BM cắt EC tại K. Chứng minh rằng .
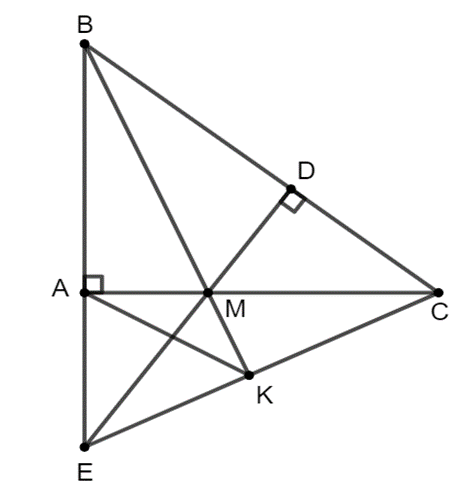
a) Xét ∆DMC vuông tại D và ∆ABC vuông tại A có chung.
Do đó ∆DMC ᔕ ∆ABC (g.g).
b) Xét ∆DBE vuông tại D và ∆DMC vuông tại D có
(cùng phụ với ).
Do đó ∆DBE ᔕ ∆DMC (g.g).
Suy ra . Do đó DB . DC = DE . DM (đpcm).
c) Xét ∆BEC có đường cao CA và BE cắt nhau tại M, suy ra M là trực tâm ∆BEC.
Do đó BK ⊥ EC.
Xét ∆EAC vuông tại A và ∆EKB vuông tại K có chung.
Do đó ∆EAC ᔕ ∆EKB (g.g)
Suy ra hay .
Xét ∆EAK và ∆ECB có và chung.
Do đó ∆EAK ᔕ ∆ECB (c.g.c).
Suy ra (các góc tương ứng).
Xem thêm các bài giải sách bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Các trường hợp đồng dạng của hai tam giác vuông
Bài 1: Mô tả xác suất bằng tỉ số