Cho tam giác ABC vuông tại A và đường cao AH. Chứng mình rằng AB2 = BH . BC

Bài 9 trang 75 SBT Toán 8 Tập 2: Cho tam giác ABC vuông tại A và đường cao AH.

a) Chứng mình rằng AB² = BH . BC.

b) Chứng mỉnh rằng AH² = BH . CH.

c) Trên tia đối của tia AC lấy điểm D (AD < AC). Đường thẳng qua H và song song với AC cắt AB, BD lần lượt tại M, N. Chứng minh rằng $\frac{MN}{MH}=\frac{AD}{AC}$.

d) Vẽ AE vuông góc với BD tại E. Chứng minh rằng $\widehat{BEH}=\widehat{BAH}$.

Trả lời

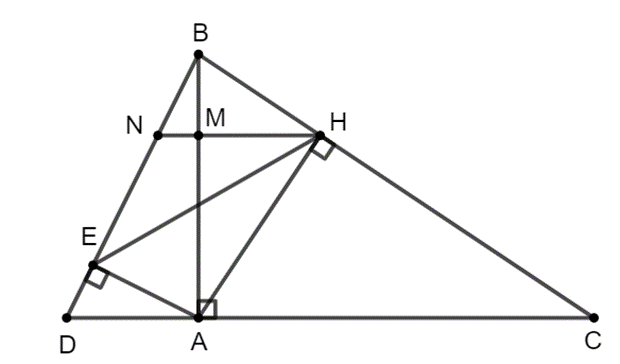
a) Xét ∆ABC vuông tại A và ∆HBA vuông tại H có $\widehat{ABC}$ chung.

Do đó ∆ABC ᔕ ∆HBA (g.g).

Suy ra $\frac{AB}{BH}=\frac{BC}{AB}$. Do đó AB² = BC . BH (đpcm).

b) Xét ∆HBA vuông tại H và ∆HAC vuông tại H có

$\widehat{BAH}=\widehat{ACH}$ (cùng phụ với $\widehat{CAH}$).

Do đó ∆HBA ᔕ ∆HAC (g.g).

Suy ra $\frac{AH}{CH}=\frac{BH}{AH}$. Do đó AH² = BH . CH (đpcm).

c) Xét ∆ABD có MN // AD, suy ra $\frac{MN}{AD}=\frac{BM}{BA}$ (1)

Xét ∆ABC có MH // AC, suy ra $\frac{MH}{AC}=\frac{BM}{BA}$ (2)

Từ (1) và (2) suy ra $\frac{MN}{AD}=\frac{MH}{AC}$. Do đó $\frac{MN}{MH}=\frac{AD}{AC}$ (đpcm).

d) Xét ∆ABD vuông tại A và ∆EBA vuông tại E có $\widehat{ABD}$ chung.

Do đó ∆ABD ᔕ ∆EBA (g.g).

Suy ra $\frac{AB}{BE}=\frac{BD}{AB}$. Do đó AB² = BD . BE.

Mà AB² = BC . BH nên BC . BH = BD . BE.

Do đó $\frac{BH}{BD}=\frac{BE}{BC}$.

Xét ∆BEH và ∆BCD có

$\frac{BH}{BD}=\frac{BE}{BC}$ và $\widehat{DBC}$ chung.

Do đó ∆BEH ᔕ ∆BCD (c.g.c).

Suy ra $\widehat{BEH}=\widehat{BCD}$ (hai góc tương ứng).

Mà $\widehat{BAH}=\widehat{BCD}$ (cùng phụ với $\widehat{HAC}$).

Do đó $\widehat{BEH}=\widehat{BAH}$ (đpcm).

Xem thêm các bài giải sách bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 3: Các trường hợp đồng dạng của hai tam giác vuông

Bài 4: Hai hình đồng dạng

Bài tập cuối chương 8

Bài 1: Mô tả xác suất bằng tỉ số

Bài 2: Xác suất lí thuyết và xác suất thực nghiệm

Bài tập cuối chương 9