Cho tam giác ABC vuông tại A có AB = 3, AC = 4, AD là đường phân giác. Tính

Bài 5 trang 69 Toán 8 Tập 2: Cho tam giác ABC vuông tại A có AB = 3, AC = 4, AD là đường phân giác. Tính:

a) Độ dài các đoạn thẳng BC, DB, DC;

b) Khoảng cách từ điểm D đến đường thẳng AC;

c) Độ dài đường phân giác AD.

Trả lời

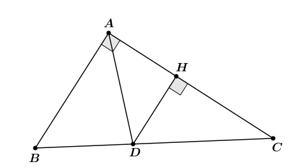
a) Xét tam giác ABC vuông tại A, theo định lí Pythagore, ta có:

BC² = AB² + AC² = 3² + 4² = 25 = 5²

Suy ra BC = 5.

Theo tính chất đường phân giác trong tam giác, ta có: $\frac{\mathrm{DB}}{\mathrm{DC}}=\frac{\mathrm{AB}}{\mathrm{AC}}$ (do AD là đường phân giác của góc BAC)

Suy ra $\frac{\mathrm{DB}}{\mathrm{BC}-\mathrm{DB}}=\frac{\mathrm{AB}}{\mathrm{AC}}$ hay $\frac{\mathrm{DB}}{5-\mathrm{DB}}=\frac{3}{4}$

Do đó 4DB = 3(5 – DB)

          4DB = 15 – 3DB

          4DB + 3DB = 15

          7DB = 15

          $\mathrm{DB}=\frac{15}{7}$

Khi đó $\mathrm{DC}=\mathrm{BC}-\mathrm{DB}=5-\frac{15}{7}=\frac{20}{7}$

Vậy $\mathrm{BC}=5;\mathrm{DB}=\frac{15}{7};\mathrm{DC}=\frac{20}{7}.$

b) Kẻ DH ⊥ AC (H ∈ AC).

Suy ra DH // AB (cùng vuông góc với AC)

Áp dụng hệ quả của định lí Thalès trong tam giác ABC với DH // AB, ta có:

$\frac{\mathrm{DH}}{\mathrm{BA}}=\frac{\mathrm{CD}}{\mathrm{CB}}$ hay $\frac{\mathrm{DH}}{3}=\frac{\frac{20}{7}}{5}$

Suy ra $\mathrm{DH}=\frac{3\cdot \frac{20}{7}}{5}=\frac{12}{7}$

Vậy khoảng cách từ điểm D đến đường thẳng AC là $\mathrm{DH}=\frac{12}{7}.$

c) Xét tam giác ABC với DH // AB, ta có: $\frac{\mathrm{AH}}{\mathrm{AC}}=\frac{\mathrm{BD}}{\mathrm{BC}}$ (hệ quả của định lí Thalès)

Hay $\frac{\mathrm{AH}}{4}=\frac{\frac{15}{7}}{5},$ suy ra $\mathrm{AH}=\frac{4\cdot \frac{15}{7}}{5}=\frac{12}{7}$

Xét tam giác AHD vuông tại H, ta có: AD² = AH² + DH² (định lí Pythagore)

Suy ra ${\mathrm{AD}}^2={\left(\frac{12}{7}\right)}^2+{\left(\frac{12}{7}\right)}^2=\frac{288}{49}$

Do đó $\mathrm{AD}=\sqrt{\frac{288}{49}}=\sqrt{\frac{144\cdot 2}{49}}=\sqrt{{\left(\frac{12\sqrt{2}}{7}\right)}^2}=\frac{12\sqrt{2}}{7}$

Vậy độ dài đường phân giác AD là $\frac{12\sqrt{2}}{7}.$

Xem thêm các bài giải SGK Toán lớp 8 Cánh Diều hay, chi tiết khác: