Cho tam giác ABC và điểm O nằm trong tam giác. Lấy M, N, P là các điểm lần lượt trên các tia OA, OB, OC sao cho OA = 3OM, OB = 3ON, OC = 3OP. Chứng minh rằng ∆ABC ᔕ ∆MNP và tìm tỉ số đồng dạn
13
29/10/2024
Cho tam giác ABC và điểm O nằm trong tam giác. Lấy M, N, P là các điểm lần lượt trên các tia OA, OB, OC sao cho OA = 3OM, OB = 3ON, OC = 3OP. Chứng minh rằng ∆ABC ᔕ ∆MNP và tìm tỉ số đồng dạng.
Trả lời
Lời giải
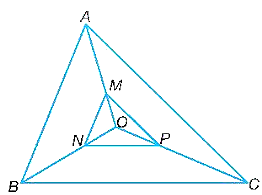
Vì OA = 3OM, OB = 3ON, OC = 3OP.
Nên \(\frac{{OA}}{{OM}} = 3;\frac{{OB}}{{ON}} = 3;\frac{{OC}}{{OP}} = 3\). Suy ra \(\frac{{OA}}{{OM}} = \frac{{OB}}{{ON}} = \frac{{OC}}{{OP}} = 3\).
Tam giác OMN có: \(\frac{{OA}}{{OM}} = \frac{{OB}}{{ON}}\).
Nên suy ra AB song song với MN (định lí Thalès đảo).
Do đó, \(\frac{{AB}}{{MN}} = \frac{{OA}}{{OM}} = 3\).
Chứng minh tương tự ta có: \(\frac{{AC}}{{MP}} = 3;\frac{{BC}}{{NP}} = 3\).
Tam giác ABC và tam giác MNP có:
\(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}} = 3\).
Do đó, ∆ABC ᔕ ∆MNP (c.c.c) với tỉ số đồng dạng 3.

