Cho tam giác ABC và các điểm M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. Chứng minh rằng ∆ABC ᔕ ∆MNP và tìm tỉ số đồng dạng.

Trả lời

Lời giải

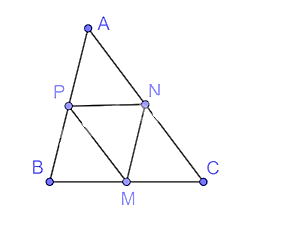
Tam giác ABC có:

M, N lần lượt là trung điểm của BC, CA

Nên MN là đường trung bình của tam giác ABC.

Do đó, MN // AB và \(\frac{{AB}}{{MN}} = 2\).

Chứng minh tương tự ta có: \(\frac{{BC}}{{PN}} = 2\); \(\frac{{AC}}{{PM}} = 2\).

Tam giác ABC và tam giác MNP có:

\(\frac{{AB}}{{MN}} = \frac{{BC}}{{PN}} = \frac{{AC}}{{PM}}\) (= 2).

Nên ∆ABC ᔕ ∆MNP (c.c.c) theo tỉ số đồng dạng là 2.