Cho hình vuông ABCD có hai đường chéo AC và BD cắt nhau tại O. Trên tia đối của tia CB lấy điểm K sao cho BC = CK. Từ điểm B kẻ đường thẳng song song với AC cắt tia DC tại E. Gọi F là trung điểm của BE.
Chứng minh các tứ giác BOCF và BDKE đều là hình vuông.
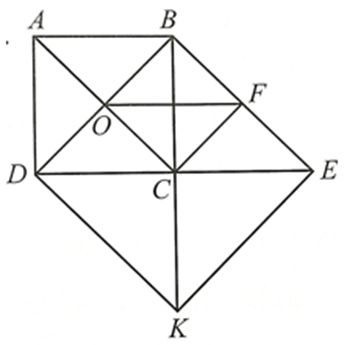
• Tứ giác ABCD là hình vuông suy ra ^ACB=45∘,OB=OC,^BOC=^DOC=90∘.
Do BE // AC suy ra ^OBF=^DOC (hai góc đồng vị) và ^CBE=^ACB=45∘ (hai góc so le trong).
Xét ∆DBC vuông tại C có: ^CDB+^CBD=90∘
Suy ra ^CDB=90∘−^CBD=90∘−45∘=45∘
Xét ∆BCE vuông tại C có: ^CBE+^CEB=90∘
Suy ra ^CBE=90∘−^CBE=90∘−45∘=45∘
Do đó ^CDB=^BEC=45∘
Tam giác BDE có: ^DBE=^DBC+^CBE=45∘+45∘=90∘ và ^CDB=^BEC=45∘
Suy ra tam giác BDE vuông cân tại B nên BD = BE
Tam giác BCE vuông tại C có ^CBE=^CEB=45∘, suy ra nên là tam giác vuông cân tại C. Do đó BC = EC
Xét ∆BCF và ∆ECF có:
BC = EC, BF = EF (do F là trung điểm của BE), cạnh CF chung
Do đó ∆BCF = ∆ECF (c.c.c). Suy ra ^BFC=^EFC=90∘.
Tứ giác BOCF có ^BOC=^OBF=^BFC=90∘ nên BOCF là hình chữ nhật.
Hình chữ nhật BOCF có OB = OC nên BOCF là hình vuông.
• Ta có: BC = CD và BC = CE nên CD = CE.
Tứ giác BDKE có hai đường chéo BK và DE cắt nhau tại trung điểm C của mỗi đường nên BDKE là hình bình hành.
Hình bình hành BDKE có ^DBE=90∘ nên BDKE là hình chữ nhật.
Hình chữ nhật BDKE có BD = BE nên BDKE là hình vuông.