Cho hình vuông ABCD. Lấy điểm E thuộc cạnh CD Chứng minh I thuộc đường thẳng BD
Cho hình vuông ABCD. Lấy điểm E thuộc cạnh CD và điểm F thuộc tia đối của tia BC sao cho BF = DE.
Chứng minh I thuộc đường thẳng BD.
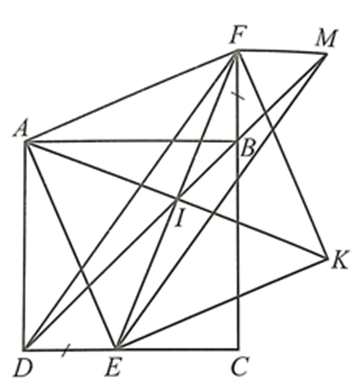
Từ điểm F kẻ đường thẳng song song với CD cắt đường thẳng BD tại M.
Do ABCD là hình vuông nên \(\widehat {CBD} = \frac{{\widehat {CBA}}}{2} = \frac{{90^\circ }}{2} = 45^\circ \).
Mà \(\widehat {FBM} = \widehat {CBD}\) (hai góc đối đỉnh), suy ra \(\widehat {FBM} = 45^\circ \).
Do MF // CD nên \(\widehat {BFM} = \widehat {BCD} = 90^\circ \) (cặp góc so le trong).
Tam giác FBM có \(\widehat {BFM} = 90^\circ \) và \(\widehat {FBM} = 45^\circ \) nên tam giác FBM vuông cân tại F.
Suy ra MF = BF.
Mà BF = DE, suy ra MF = DE.
Tứ giác DEMF có MF = DE và MF // DE nên DEMF là hình bình hành.
Mà I là trung điểm của EF, suy ra I là trung điểm của DM.
Vậy I thuộc đường thẳng DM hay I thuộc đường thẳng BD.