Cho hình bình hành ABCD. Ở phía ngoài hình bình hành, vẽ các hình vuông ABEF và ADGH (Hình 26).

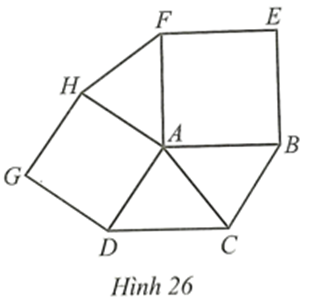
Chứng minh:

AC ⊥ HF.

Ta có: \(\widehat {HAK} + \widehat {DAH} + \widehat {DAC} = \widehat {CAK} = 180^\circ \) và \(\widehat {DAH} = 90^\circ \) nên \(\widehat {HAK} + \widehat {DAC} = 90^\circ \).

Mà \(\widehat {AHF} = \widehat {DAC}\) (vì DHAF = DADC chứng minh câu a), suy ra \(\widehat {HAK} + \widehat {AHF} = 90^\circ \).

Trong tam giác AHK, ta có: \(\widehat {AKH} + \widehat {HAK} + \widehat {AHF} = 180^\circ \).

Suy ra \(\widehat {AKH} = 180^\circ - \left( {\widehat {HAK} + \widehat {AHF}} \right) = 180^\circ - 90^\circ = 90^\circ \).

Vậy AK ⊥ HK hay AC ⊥ HF.